题目内容
如图，A、B、C、D、E、都是⊙O上的点，AB=BC=CD，∠BCD=130°，求∠AED度数．考点：圆周角定理
专题：
分析：连接AD，OA、OB、OC、OD，根据四边形ABCD是圆内接四边形即可求得∠BAD的度数，然后根据圆周角定理求得∠BOD的度数，进而求得∠AOD的度数，则∠AED即可求得．
解答：
解：连接AD，OA、OB、OC、OD．
∵四边形ABCD是圆内接四边形，
∴∠BAD=180°-∠BCD=180°-130°=50°，
∴∠BOD=2∠BAD=100°，
又∵AB=BC=CD，
∴∠AOB=∠BOC=∠CDO=50°，
∴∠AOD=150°，
∴∠AED=75°．
解：连接AD，OA、OB、OC、OD．∵四边形ABCD是圆内接四边形，
∴∠BAD=180°-∠BCD=180°-130°=50°，
∴∠BOD=2∠BAD=100°，
又∵AB=BC=CD，
∴∠AOB=∠BOC=∠CDO=50°，
∴∠AOD=150°，
∴∠AED=75°．
点评：本题考查了圆周角定理以及圆的内接四边形的性质，正确作出辅助线，构造圆内接四边形是关键．
练习册系列答案
阅读快车系列答案
相关题目
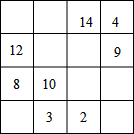将1～16这16个整数填入4×4的正方形表格中，使得每行、每列、每条对角线上四个数之和都相等，如图所示，恰有8个小方格中填的数被一个淘气的小朋友擦掉了，请你将擦掉的这8个数设法恢复出来．
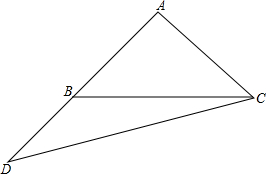如图，在△ABC中，AB=AC，∠ABC=40°，延长AB到D，使得AD=BC，连结CD，求∠D的度数．