题目内容
2. 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.(1)直接写出实际每月的销售量p(台)与月份x之间的函数关系式;
(2)求前三个月中每月的实际销售利润w(万元)与月份x之间的函数关系式;
(3)试判断全年哪一个月的售价最高,并指出最高售价.
分析 (1)要根据自变量的不同取值范围,运用待定系数法分段计算出p与x的函数关系式;
(2)可根据实际销售利润=单件的利润×销售的数量,然后根据题目中给出的售价与月次的函数式以及(1)中销售量与月次的关系式,得出实际销售利润与月次的函数关系式;
(3)要根据自变量的不同的取值范围分别进行讨论,然后找出最高售价.
解答 解:(1)由题意得:
P=$\left\{\begin{array}{l}{-5x+40(1≤x<4且x为整数)}\\{2x+12(4≤x≤12且x为整数)}\end{array}\right.$;
(2)w=(-0.05x+0.25-0.1)(-5x+40)
=$\frac{1}{4}$(x-3)(x-8)
=$\frac{1}{4}$x2-$\frac{11}{4}$x+6,
即w与x间的函数关系式w=$\frac{1}{4}$x2-$\frac{11}{4}$x+6;
(3)①当1≤x<4时,y=-0.05x+0.25中y随x的增大而减小,
∴x=1时,y最大=0.2;
②当4≤x≤6时,y=0.1万元,保持不变;
③当6<x≤12时,y=0.015x+0.01中y随x的增大而增大,
∴x=12时,y最大=0.015×12+0.01=0.19.
综合得:全年1月份售价最高,最高为0.2万元/台.
点评 本题是利用一次函数和二次函数的有关知识解答实际应用题,是中考的常见题型,借助函数图象表达题目中的信息,读懂图象是关键.

练习册系列答案
相关题目
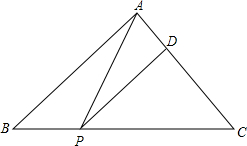 如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?
如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?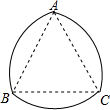 如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.
如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长. 如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,
如图,已知AB是⊙O的直径,AB=10,点C、D在⊙O上,DC平分∠ACB,点E在⊙O外,



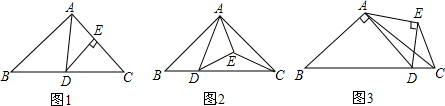
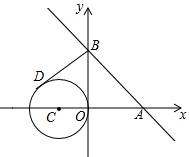 如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.
如图,直线y=-x+2与x轴、y轴分别交于点A,B,C(-1,0),且圆C的半径为1.若BD切圆C于点D,点D在第二象限,求点D的坐标.