题目内容
7.在同一坐标系下,函数y=m(x-1)与y=mx2+mx+m的图象只可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 关键是m的正负的确定,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=-$\frac{b}{2a}$,与y轴的交点坐标为(0,c).
解答 解:A.由函数y=m(x-1)的图象可知m>0,即函数y=mx2+mx+m开口方向朝上,交于y轴的正半轴,与图象不符,故A选项错误;
B.由函数y=m(x-1)的图象可知m>0,即函数y=m(x-1)交于y轴的负半轴,与图象不符,故B选项错误;
C.由函数y=m(x-1)的图象可知m<0,即函数y=mx2+mx+m开口方向朝下,交于y轴的负半轴,对称轴为x=-$\frac{b}{2a}$=-$\frac{1}{2}$,与图象相符,故C选项正确;
D.由函数y=m(x-1)的图象可知m<0,即函数y=mx2+2x+2开口方向朝下,对称轴为x=-$\frac{b}{2a}$=-$\frac{1}{2}$<0,与图象相符,故D选项错误.
故选:C.
点评 主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力,要掌握它们的性质才能灵活解题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目

 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.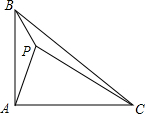 在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点,PA=2,PB=1,PC=3,求∠APB的度数.
在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点,PA=2,PB=1,PC=3,求∠APB的度数.