题目内容
13.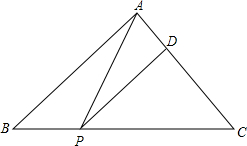 如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?
如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?
分析 首先根据在△ABC中,已知BC=4,AC=2$\sqrt{3}$,∠C=60°,设PB=x,列出△APD的面积关于x的二次函数,利用配方法求得最大值,即为所求△APD的面积最大值.
解答  解:设BP=x,则PC=4-x,过点A作AH⊥AC于点H,
解:设BP=x,则PC=4-x,过点A作AH⊥AC于点H,
∵∠C=60°,∴∠HPC=30°,
∴PH=$\frac{\sqrt{3}}{2}$(4-x),
∵AB∥PD,
∴PB:BC=AD:AC,
∴AD=$\frac{\sqrt{3}x}{2}$,
∴S△PAD=$\frac{1}{2}$AD•PH=$\frac{1}{2}×$$\frac{\sqrt{3}}{2}$x•$\frac{\sqrt{3}}{2}$(4-x)=-$\frac{3}{8}$(x-2)2+$\frac{3}{2}$,
当x=2时,△APD的面积最大,
∴PB=2时,△APD的面积最大,最大面积为:$\frac{3}{2}$.
点评 本题考查三角形面积的计算、三角函数、直角三角形的性质.解决本题的关键点是证得△ABC为Rt△,从而利用三角函数建立起边间的关系;并在解题过程中转化成求二次函数的最值问题.

练习册系列答案
相关题目
6.已知a2-ab=20,ab-b2=-12,则a2-b2和a2-2ab+b2的值分别为( )
| A. | -8和32 | B. | 8和32 | C. | -32和32 | D. | 8和-32 |
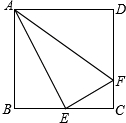 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.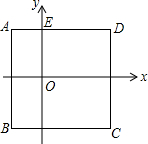 如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来.
如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来.
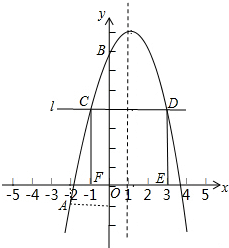 如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点. 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.