题目内容
10.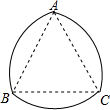 如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.
如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.
分析 连接OB、OC,作OD⊥BC于D,根据正三角形的有关计算求出弧的半径和圆心角,根据弧长的计算公式求解即可.
解答 解: 连接OB、OC,作OD⊥BC于D,
连接OB、OC,作OD⊥BC于D,
∵△ABC是正三角形,
∴∠BOC=120°,
∴∠BOD=60°,又BD=$\frac{1}{2}$BC=1,
∴OB=$\frac{2\sqrt{3}}{3}$,
∴$\widehat{BC}$的长为:$\frac{120π×\frac{2\sqrt{3}}{3}}{180}$=$\frac{4\sqrt{3}}{9}$π,
∴弧三角形的周长=$\frac{4\sqrt{3}}{9}$π×3=$\frac{4\sqrt{3}}{3}$π.
点评 本题考查的是正多边形和圆的知识,理解弧三角形的概念、掌握正多边形的中心角的求法是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.
如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.
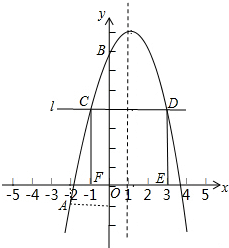 如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点. 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势. 如图,BE、CE分别为△ABC的两个外角平分线,EP⊥AM于P,EQ⊥AN于Q
如图,BE、CE分别为△ABC的两个外角平分线,EP⊥AM于P,EQ⊥AN于Q