题目内容
9.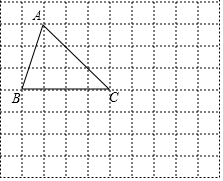 如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)
如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.(注:顶点在网格线交点处的三角形叫做格点三角形)(1)图中AC边上的高为2$\sqrt{2}$个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:以点C为位似中心,作△DEC∽△ABC,且相似比为1:2.
分析 (1)利用面积法计算AC边上的高;
(2)取BC的中点E,过E作DE∥AB交AC于F,则△DEC满足条件;或延长BC到E′使CE′=$\frac{1}{2}$BC,作E′D′∥AB交AC的延长线于D′,则△D′E′C满足条件.
解答 解:(1)设AC边上的高为h,
则$\frac{1}{2}$AC•h=$\frac{1}{2}$BC•3,
所以h=$\frac{3×4}{3\sqrt{2}}$=2$\sqrt{2}$,
故答案为2$\sqrt{2}$;
(2)如图,△DEC和△D′E′C为所作.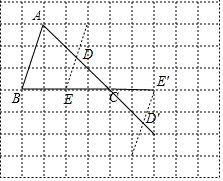
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
4.抛物线y=-2(x-1)2-3与y轴交点的横坐标为( )
| A. | -3 | B. | -4 | C. | -5 | D. | -1 |
14.若等腰三角形中有一个角等于40°,则这个等腰三角形顶角的度数为( )
| A. | 40° | B. | 100° | C. | 40°或100° | D. | 40°或70° |
1.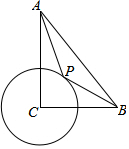 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
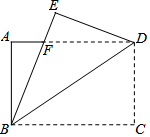 如图,将矩形纸片ABCD沿对角线BD折叠,点C的对应点为E,BE交AD于点F.
如图,将矩形纸片ABCD沿对角线BD折叠,点C的对应点为E,BE交AD于点F.


