题目内容
1.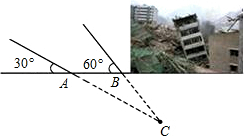 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)
分析 根据锐角三角函数可以求得点C到地面的距离,从而可以解答本题.
解答 解:如图所示,过点C作CD⊥AB,交AB的延长线于点D,
由题意可知,∠CAD=30°,∠CBD=60°,
设CD=x米,
则BD=$\frac{x}{tan60°}$,AD=$\frac{x}{tan30°}$,
∵AB=2米,AD=AB+BD,
∴AD=2+BD,
∴2+$\frac{x}{tan60°}$=$\frac{x}{tan30°}$,
解得,x≈1.7
即生命所在点C的深度是1.7米.
点评 本题考查解直角三角形的应用,解答本题的关键是明确题意,利用锐角三角函数解答.

练习册系列答案
相关题目
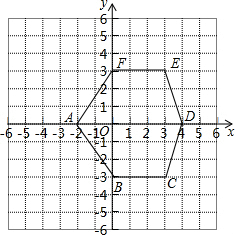 如图是一个平面直角坐标系,按要求完成下列各小题.
如图是一个平面直角坐标系,按要求完成下列各小题.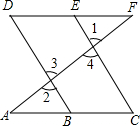 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由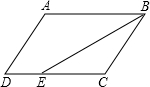 如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长.
如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长. 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.