题目内容
4.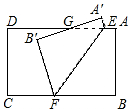 如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.
如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.
分析 根据AE∥BF,可得∠AEF+∠BFE=180°,再根据折叠变换的性质得:∠BFE=∠B'FE,而∠CFB′=50°,进而得到∠BFE=(180°-50°)÷2=65°,最后得出∠AEF=180°-65°=115°.
解答  解:如图,∵四边形ABCD为长方形,
解:如图,∵四边形ABCD为长方形,
∴AE∥BF,
∴∠AEF+∠BFE=180°,
由折叠变换的性质得:
∠BFE=∠B'FE,而∠CFB′=50°,
∴∠BFE=(180°-50°)÷2=65°,
∴∠AEF=180°-65°=115°.
故答案为:115°.
点评 本题主要考查了翻折变换的性质、矩形的性质、平行线的性质,解决问题的关键是掌握矩形的性质、平行线的性质等几何知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在数轴上表示数a,b的点都在原点的右侧,表示数c的点在原点的左侧,表示数a的点离远点最远,表示数b的点离原点最近,请将a,-a,b,-b,c,-c用“>”连接起来:a>-c>b>-b>c>-a.
16.下列命题正确的是( )
①三角形中最大内角一定不小于60°; ②所有等腰直角三角形都相似;
③正多边形的外角为24°,则它的中心角也为24°; ④顺次连接对角线相等的四边形各边中点得到矩形.
①三角形中最大内角一定不小于60°; ②所有等腰直角三角形都相似;
③正多边形的外角为24°,则它的中心角也为24°; ④顺次连接对角线相等的四边形各边中点得到矩形.
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②④ |
14.为了解某县八年级9800名学生的视力情况,从中抽查了100名学生的视力情况,对于这个问题,下面说法中正确的是( )
| A. | 9800名学生是总体 | |
| B. | 每个学生是个体 | |
| C. | 100名学生是所抽取的一个样本 | |
| D. | 100名学生的视力情况是所抽取的一个样本 |
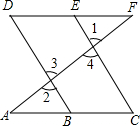 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
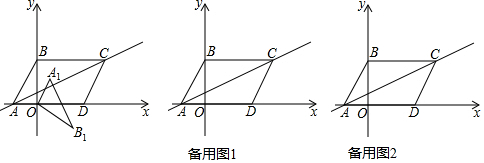
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由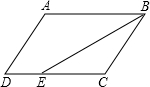 如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长.
如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长.