题目内容
7.在三角形ABC中,∠A=80°,OB、OC分别平分∠ABC和∠ACB,你能求出∠BOC的度数.分析 根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线的定义得到∠0BC=$\frac{1}{2}$∠ABC,∠0CB=$\frac{1}{2}$∠ACB,根据三角形内角和定理计算即可.
解答 解:∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵OB、OC分别平分∠ABC和∠ACB,
∴∠0BC=$\frac{1}{2}$∠ABC,∠0CB=$\frac{1}{2}$∠ACB,
∴∠BOC=180°-(∠0BC+∠0CB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-50°=130°.
点评 本题考查的是三角形内角和定理、角平分线的定义,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
17.抛物线y=(x-m)2+n可以由抛物线y=x2向上平移2个单位,再向左平移3个单位得到,则m-n值为( )
| A. | -6 | B. | -5 | C. | -1 | D. | 1 |
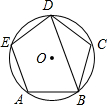 如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.
如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.
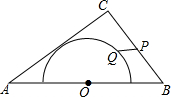 如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5.
如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5.