题目内容
16.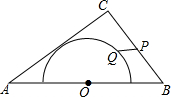 如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5.
如图,在△ABC中,AB=5,AC=4,BC=3,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是4.5.
分析 设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,此时垂线段OP1最短,P1Q1最小值为OP1-OQ1,求出OP1,如图当Q2在AB边上时,P2与B重合时,P2Q2最大值=2.5+1.5=4,由此不难解决问题.
解答 解:如图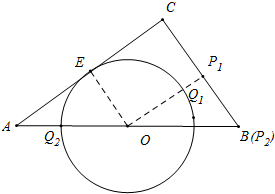 ,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OP1-OQ1,
∵AB=5,AC=4,BC=3,
∴AB2=AC2+BC2,
∴∠C=90°,
∵∠OP1B=90°,
∴OP1∥AC
∵AO=OB,
∴P1C=P1B,
∴OP1=$\frac{1}{2}$AC=2,
∴P1Q1最小值为OP1-OQ1=0.5,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=2.5+1.5=4,
∴PQ长的最大值与最小值的和是4.5.
故答案为:4.5.
点评 本题考查切线的性质、三角形中位线定理等知识,解题的关键是正确找到点PQ取得最大值、最小值时的位置,属于中考常考题型.

练习册系列答案
相关题目
6.在-$\frac{1}{2}$,-$\frac{1}{3}$,-2,-1这四个数中,最大的数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
5.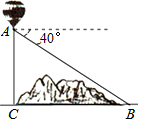 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )| A. | asin40°米 | B. | acos40°米 | C. | atan40°米 | D. | $\frac{a}{tan40°}$米 |
 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.