题目内容
18.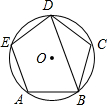 如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.
如图,正五边形ABCDE为内接于⊙O的,则∠ABD=72°.
分析 根据多边形内角和定理、正五边形的性质求出∠ABC、CD=CB,根据等腰三角形的性质求出∠CBD,计算即可.
解答 解:∵五边形ABCDE为正五边形,
∴∠ABC=∠C=$\frac{(5-2)×180°}{5}$=108°,
∵CD=CB,
∴∠CBD=$\frac{180°-108°}{2}$=36°,
∴∠ABD=∠ABC-∠CBD=72°,
故答案为:72°.
点评 本题考查的是正多边形和圆、多边形的内角和定理,掌握正多边形和圆的关系、多边形内角和等于(n-2)×180°是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.在-$\frac{1}{2}$,-$\frac{1}{3}$,-2,-1这四个数中,最大的数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
13.已知等腰三角形一腰上的中线将它的周长分成9cm和12cm两部分,则等腰三角形的底边长为( )
| A. | 9cm | B. | 5cm | C. | 6cm或5cm | D. | 5cm或9cm |
10.某人去水果批发市场采购苹果,他看中了A、B两家苹果、这两家苹果品质一样,零售价都为10元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
(1)如果他批发60千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
| 数量范围(千克) | 0~50 | 50以上~150的部分 | 150以上~250的部分 | 250以上的部分 |
| 价格(元) | 零售价的90% | 零售价的80% | 零售价的70% | 零售价的60% |
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
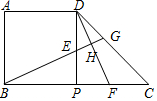 ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.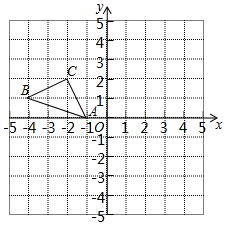 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: