题目内容
17.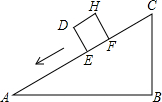 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.
分析 根据已知得出设AE=x米,可得EC=(12-x)米,利用勾股定理得出DC2=DE2+EC2=4+(12-x)2,AE2+BC2=x2+36,即可求出x的值.
解答 解:如图,连接CD,
设AE=x米,
∵坡角∠A=30°,∠B=90°,BC=6米,
∴AC=12米,
∴EC=(12-x)米,
∵正方形DEFH的边长为2米,即DE=2米,
∴DC2=DE2+EC2=4+(12-x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(12-x)2=x2+36,
解得:x=$\frac{14}{3}$米,
答:当AE为$\frac{14}{3}$米时,有DC2=AE2+BC2.
点评 此题主要考查了勾股定理的应用以及一元二次方程的应用,根据已知表示出CE,AE的长度是解决问题的关键.

练习册系列答案
相关题目
7.若两条平行线被第三条直线所截,则一对内错角的角平分线互相 ( )
| A. | 垂直 | B. | 平行 | C. | 重合 | D. | 相交 |
8.具备下列条件的三角形中,不能为直角三角形的是( )
| A. | ∠A+∠B=∠C | B. | ∠A=∠B=∠C/2 | C. | ∠A=90°-∠B | D. | ∠A-∠B=90° |
9.下列根式是最简二次根式的是( )
| A. | $\sqrt{48}$ | B. | $\sqrt{{a^2}+{b^2}}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{4x+8}$ |
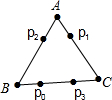 小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.
小明观看了阿尔法狗下围棋后,设计了一款电子跳蚤游戏,如图所示的正△ABC边长为12cm,如果电子跳蚤开始在BC边的点P0处,且BP0=4cm.此时第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步P2从跳到BC边的P3(第3次落点)处,且BP3=BP2;…:电子跳蚤按照上述规则已知跳下去,第n次落点为Pn(n为正整数),则点P2015与点P2016之间的距离是4cm.