题目内容
8.具备下列条件的三角形中,不能为直角三角形的是( )| A. | ∠A+∠B=∠C | B. | ∠A=∠B=∠C/2 | C. | ∠A=90°-∠B | D. | ∠A-∠B=90° |
分析 在A、B、C条件下,利用三角形内角和定理可推出∠C=90°,在D的条件下可推出∠A是钝角.
解答 解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°.
∴△ABC是直角三角形;
②∵∠A=∠B=$\frac{1}{2}$∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°.
∴△ABC是直角三角形;
③∵∠A=90°-∠B,∠A+∠B+∠C=180°,
∴∠C=90°.
∴△ABC是直角三角形;
④∵∠A-∠B=90°,
∴∠A=90°+∠B>90°,
∴△ABC是钝角三角形.
故选D.
点评 本题主要考查了三角形内角和定理,涉及到三角形的内角时,通常与三角形内角和定理和外角的性质相联系.

练习册系列答案
相关题目
16.方程x2=3x的解是( )
| A. | x=-3 | B. | x=3 | C. | x1=0,x2=3 | D. | x1=0,x2=-3 |
 南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).
南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).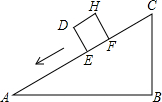 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE为多少米时?有DC2=AE2+BC2.