题目内容
15.如图,在平面直角坐标系中,点B在y轴正半轴上且∠ABO=30°,D(2,0),直线y=$\frac{\sqrt{3}}{4}$(x+1)的图象过点C(3,n),与x轴交于点A.(1)直接写出A点坐标(-1,0),B点坐标(0,$\sqrt{3}$),n=3;
(2)求证:四边形ABCD为平行四边形;
(3)将△AOB绕点O按顺时针方向旋转120°到△A1OB1,求A1的坐标;
(4)将△AOB绕点O按顺时针方向旋转到△A2OB2,直接写出以点O、A2、D、B2为顶点的四边形为平行四边形时A2的坐标.
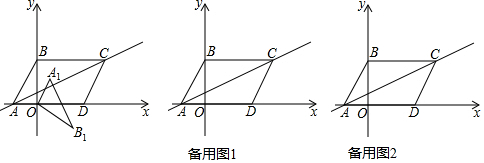
分析 (1)求出直线y=$\frac{\sqrt{3}}{4}$(x+1),当y=0时,x=-1,得出∴A(-1,0),OA=1,由直角三角形的性质和勾股定理得出OB=$\sqrt{3}$OA=$\sqrt{3}$,得出B(0,$\sqrt{3}$),把点C坐标代入直线解析式求出n即可;
(2)由(1)得:C(3,$\sqrt{3}$),B(0,$\sqrt{\sqrt{3}}$),得出BC∥AD,BC=3,求出AD=OA+OD=3,得出BC=AD,即可证出四边形ABCD为平行四边形;
(3)作A1E⊥OB于E,由旋转的性质得:OA1=OA=1,∠AOA1=120°,求出∠A1OE=30°,得出A1E=$\frac{1}{2}$OA1=$\frac{1}{2}$,求出OE=$\sqrt{3}$A1E=$\frac{\sqrt{3}}{2}$,即可得出A1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(4)分三种情况:当点A2在第一象限时,旋转角为120°;点A2在第四象限时,旋转角为240°;点A2在第二象限时,旋转角为420°;分别由平行四边形的性质求出点A2的坐标即可.
解答 解:(1)∵直线y=$\frac{\sqrt{3}}{4}$(x+1),当y=0时,x=-1,
∴A(-1,0),OA=1,
∵∠ABO=30°,∠AOB=90°,
∴AB=2OA=2,
∴OB=$\sqrt{3}$OA=$\sqrt{3}$,
∴B(0,$\sqrt{3}$),
把点C(3,n)代入直线y=$\frac{\sqrt{3}}{4}$(x+1)得:n=$\frac{\sqrt{3}}{4}$(3+1)=$\sqrt{3}$,
故答案为:-1,0;0,$\sqrt{3}$;3;
(2)由(1)得:C(3,$\sqrt{3}$),B(0,$\sqrt{\sqrt{3}}$),
∴BC∥AD,BC=3,
∵AD=OA+OD=3,
∴BC=AD,
∴四边形ABCD为平行四边形;
(3)作A1E⊥OB于E,如图所示:
由旋转的性质得:OA1=OA=1,∠AOA1=120°,
∴∠A1OE=120°-90°=30°,
∴A1E=$\frac{1}{2}$OA1=$\frac{1}{2}$,
∴OE=$\sqrt{3}$A1E=$\frac{\sqrt{3}}{2}$,∴A1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
(4)当点A2在第一象限时,以点O、A2、D、B2为顶点的四边形为平行四边形时,A2($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
点A2在第四象限时,以点O、A2、D、B2为顶点的四边形为平行四边形时,A2($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$);
点A2在第二象限时,以点O、A2、D、B2为顶点的四边形为平行四边形时,A2(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
综上所述:以点O、A2、D、B2为顶点的四边形为平行四边形时A2的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)或(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题是三角形综合题目,考查了坐标与图形性质、含30°角的直角三角形的性质、勾股定理、一次函数的应用、平行四边形的判定与性质、旋转的性质等知识;本题综合性强,有一定难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{4}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{9}$ |
(1)若某工厂每月支付的工人工资为220000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,根据题设完成下列表格,并列方程求解
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
| 工种 | 工人每月工资(元) | 招聘人数 | 工厂应付工人的约工资(元) |
| A | 1600 | x | 1600x |
| B | 2000 | 120-x | 2000(120-x) |
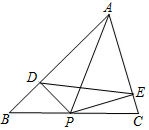 如图,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,点P是BC上一动点,PD⊥AB于D,PE⊥AC于E,则线段DE的最小值为$\sqrt{3}$.
如图,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,点P是BC上一动点,PD⊥AB于D,PE⊥AC于E,则线段DE的最小值为$\sqrt{3}$.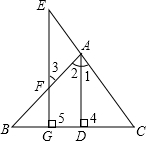 根据题意结合图形填空:
根据题意结合图形填空: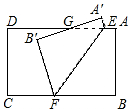 如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.
如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.