题目内容
16.若a=-$\sqrt{(-3)^{2}}$,b=-|$\root{3}{-2}$|,c=-$\root{3}{(-2)^{3}}$,则a,b,c的大小关系是a<b<c.分析 先将a,b,c的值化简,再根据实数的比较大小的方法解答即可.
解答 解:∵a=$-\sqrt{(-3)^{2}}$=-3,b=$-|\root{3}{-2}|$=$\root{3}{2}$,c=$-\root{3}{(-2)^{3}}$=2,
∴a<b<c.
故答案为:a<b<c.
点评 本题主要考查实数的大小比较及其实数的性质,能根据实数的性质将式子化简是解决此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点…像这样,10条直线相交,最多交点的个数是( )
如图,两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点…像这样,10条直线相交,最多交点的个数是( )
 如图,两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点…像这样,10条直线相交,最多交点的个数是( )
如图,两条直线相交,最多有一个交点;三条直线相交,最多有三个交点;四条直线相交,最多有6个交点…像这样,10条直线相交,最多交点的个数是( )| A. | 40个 | B. | 45个 | C. | 50个 | D. | 55个 |
1.下列方程中,两根分别为2和3的方程是( )
| A. | x2-x-6=0 | B. | x2-6x+5=0 | C. | x2+x-6=0 | D. | x2-5x+6=0 |
 如图,在Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,CD=2,则BE的长为2.
如图,在Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,CD=2,则BE的长为2.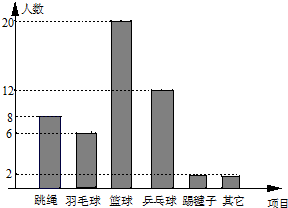 小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )
小程对本班50名同学进行了“我最喜爱的运动项目”的调查,统计出了最喜爱跳绳、羽毛球、篮球、乒乓球、踢毽子等运动项目的人数,并根据调查结果绘制了如图所示的条形统计图.若将条形统计图转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为( )