题目内容
18.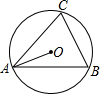 如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的大小为70度.
如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的大小为70度.
分析 连接OB.根据等腰△OAB的两个底角∠OAB=∠OBA、三角形的内角和定理求得∠AOB的度数,然后由圆周角定理求即可得∠C的度数.
解答 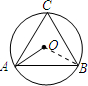 解:连接OB.
解:连接OB.
在△OAB中,OA=OB(⊙O的半径),
∴∠OAB=∠OBA(等边对等角);
又∵∠OAB=20°,
∴∠OBA=20°;
∴∠AOB=180°-2×20°=140°;
而∠C=$\frac{1}{2}$∠AOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠C=70°,
故答案是:70.
点评 本题主要考查了三角形的内角和定理、圆周角定理.解答此类题目时,经常利用圆的半径都相等的性质,将圆心角置于等腰三角形中解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,在△ABC中,DE∥BC,分别交AB、AC于点D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,则下列选项中错误的是( )
如图,在△ABC中,DE∥BC,分别交AB、AC于点D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,则下列选项中错误的是( )
 如图,在△ABC中,DE∥BC,分别交AB、AC于点D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,则下列选项中错误的是( )
如图,在△ABC中,DE∥BC,分别交AB、AC于点D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,则下列选项中错误的是( )| A. | △ADE∽△ABC | B. | BC=10 | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{2}{3}$ | D. | $\frac{△ADE的面积}{四边形DBCE的面积}$=$\frac{4}{21}$ |
10.下列各图中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
8.使(x2+px+8)(x2-3x+q)乘积中不含x2和x3项的p,q的值分别是( )
| A. | p=3,q=1 | B. | p=-3,q=-9 | C. | p=0,q=0 | D. | p=-3,q=1 |
 已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.
已知,如图,在Rt△ABC中,AC=6,BC=8,D边AB上一点,连接CD,过点D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,连接B1C.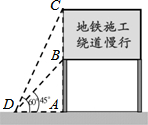 某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.
某市备受关注的地铁六号线正紧张施工,为了缓解一些施工路段交通拥挤的现状,交警队设立了如图所示的交通略况显示牌,已知立杆AB的高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°,求路况显示牌BC的高度.