题目内容
11.已知a=$\sqrt{5}-\sqrt{2}$,b=$\sqrt{5}+\sqrt{2}$,求$\frac{a}{b}$+$\frac{b}{a}$的值.分析 先求出a+b,ab,然后通分,恒等变形,利用整体代入的思想解决问题.
解答 解:∵a=$\sqrt{5}-\sqrt{2}$,b=$\sqrt{5}+\sqrt{2}$,
∴a+b=2$\sqrt{5}$,ab=5-2=3,
∴原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{20-6}{3}$=$\frac{14}{3}$.
点评 本题考查二次根式的化简求值,乘法公式,解题的关键是学会灵活运用公式,体现了整体代入的思想,属于中考常考题型.

练习册系列答案
相关题目
6.下列二次根式中,与$\sqrt{8}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
 已知:如图,BC∥AD,∠A=∠B.
已知:如图,BC∥AD,∠A=∠B.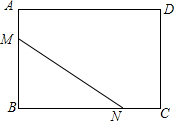 如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.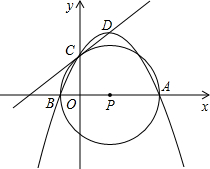 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P. 将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°.
将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=110°. 如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E.求证:AC是⊙O的切线.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E.求证:AC是⊙O的切线.