题目内容
1.2014年,某公司A、B两个部门分别有职工50人和75人,2015年元月为减员增效,公司决定对两个部门按照相同的比例进行裁员分流,使公司A、B两个部门一共留下100人,裁员分流后,大大激发了职员工的积极性,公司效益明显好转.据公司2015年财务报表显示:2015年度A部门创下产值620万元,与2014年度相比,A部门的人均产值增加了4.5万元,B部门的产值增加了30万元,且B部门人均产值的增加量比全公司的人均产值的增加量少1万元.据预测:2016年度,公司发展又将迈上一个新台阶,该公司总产值将达到1210万元,且2014年度到2016年度这两年的全公司年度总产值平均增长率与2015年到2016年A部门人均产值增长率相同.(1)求A部门裁员后留下了多少人?
(2)求2014年B部门的总产值是多少万元?
(2)根据预测估计2016年该公司A部门人均产值将达到多少万元?
分析 (1)设A部门裁员后留下了m人,则B部门裁员后留下了(100-m)人,根据两个部门按照相同的比例进行裁员分流,即可得出关于m的一元一次方程,解之即可得出结论;
(2)设2014年B部门的总产值是x万元,则2015年B部门的总产值是(x+30)万元,2014年A部门的总产值是(620÷40-4.5)×50=550万元,根据B部门人均产值的增加量比全公司的人均产值的增加量少1万元,即可得出关于x的一元一次方程,解之即可得出结论;
(3)设2014年度到2016年度这两年的全公司年度总产值平均增长率为a,根据2014年及2016年的全公司年度总产值,即可得出关于a的一元二次方程,解之即可得出a值,再根据2014年度到2016年度这两年的全公司年度总产值平均增长率与2015年到2016年A部门人均产值增长率相同可求出2016年该公司A部门人均产值.
解答 解:(1)设A部门裁员后留下了m人,则B部门裁员后留下了(100-m)人,
根据题意得:$\frac{m}{50}$=$\frac{100-m}{75}$,
解得:m=40.
答:A部门裁员后留下了40人.
(2)设2014年B部门的总产值是x万元,则2015年B部门的总产值是(x+30)万元,2014年A部门的总产值是(620÷40-4.5)×50=550万元,
根据题意得:$\frac{x+30}{100-40}$-$\frac{x}{75}$=$\frac{620+x+30}{100}$-$\frac{550+x}{50+75}$-1,
解得:x=450.
答:2014年B部门的总产值是450万元.
(3)设2014年度到2016年度这两年的全公司年度总产值平均增长率为a,
根据题意得:(450+550)(1+a)2=1210,
解得:a=0.1=10%或a=-2.1(舍去),
∴2016年该公司A部门人均产值为620÷40×(1+10%)=17.05(万元).
答:2016年该公司A部门人均产值将达到17.05万元.
点评 本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:(1)根据两个部门按照相同的比例进行裁员分流,列出关于m的一元一次方程;(2)根据B部门人均产值的增加量比全公司的人均产值的增加量少1万元,列出关于x的一元一次方程;(3)根据2014年及2016年的全公司年度总产值,列出关于a的一元二次方程.

 阅读快车系列答案
阅读快车系列答案| A. | -4ab | B. | 4ab | C. | 4a2b2 | D. | 4a2b |
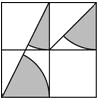 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )| A. | $\frac{1}{4}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{8}$π | D. | $\frac{3}{8}$π |
| A. | $\frac{1}{2017}$ | B. | -$\frac{1}{2017}$ | C. | -2017 | D. | 2017 |
| A. | (a2)3=a5 | B. | 3a2-a2=3 | C. | a3•a6=a9 | D. | (2a2)2=4a2 |
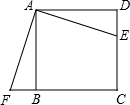 如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.