题目内容
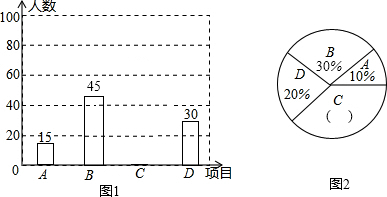
13.为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:(1)请计算本次调查中的学生人数是150.
扇形统计图中C所在扇形的圆心角度数为144°,并补全条形统计图;
(2)参加跳绳的30名同学中,有4名女生,现将这30名学生分成两组进行对抗练习,且4名女生每组分两人,求小红和美美能分在同一组的概率.
分析 (1)根据A项目的人数及其百分比可得总人数,用360°乘以C项目的百分比可得其圆心角度数,总人数乘以C项目的百分比可得其人数;
(2)列出所有等可能结果,根据概率公式可得答案.
解答 解:(1)本次调查中的学生人数是15÷10%=150(人),
扇形统计图中C所在扇形的圆心角度数为360°×(1-10%-30%-20%)=144°,
C项目的人数为150×(1-10%-30%-20%)=60,
补全图象如下:
故答案为:150,144;
(2)记这四位同学分别为A、B、C、D,其中C表示小红,D表示美美,
两人一组有如下6种情况:AB、AC、AD、BC、BD、CD,
其中小红和美美能分在同一组的有AB、CD两种可能结果,
∴小红和美美能分在同一组的概率为$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题主要考查条形统计图与扇形统计图及概率公式,根据条形统计图和扇形统计图得出解题所需的数据及概率公式是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.某玩具厂生产一种玩具,据市场调查,若按每个玩具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个玩具的固定成本Q(元)与月销量y(个)满足如下关系:
(1)写出月销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的比例是多少?(用分数表示)
(4)若该厂这种玩具的月销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的比例是多少?(用分数表示)
(4)若该厂这种玩具的月销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
2.下列数中比$\sqrt{5}$大的是( )
| A. | -3 | B. | 0 | C. | 4 | D. | 2 |