题目内容
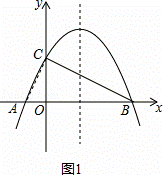
如图,已知抛物线y=﹣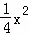 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
(1)求抛物线的解析式及其对称轴方程.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D的坐标和△DBC的面积;若不存在,请说明理由.
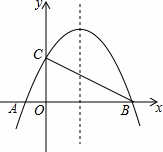
考点: 二次函数综合题.
分析: (1)直接把点B(8,0)代入抛物线y=﹣ +bx+4,求出b的值即可得出抛物线的解析式,进而可得出其对称轴方程;
+bx+4,求出b的值即可得出抛物线的解析式,进而可得出其对称轴方程;
(2)求出A点坐标,再由锐角三角函数的定义得出tan∠ACO=tan∠CBO,故∠ACO=∠CBO,由此可得出结论;
(3)求出BC解析式,将S△BCD转化为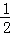 DH•OB,设D(t,﹣
DH•OB,设D(t,﹣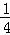 t2+
t2+ t+4),H(t,﹣
t+4),H(t,﹣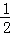 t+4),面积可转化为S△BCD=﹣
t+4),面积可转化为S△BCD=﹣ (t﹣4)2+2,△DBC的最大面积为2,此时D点坐标为(4,6).
(t﹣4)2+2,△DBC的最大面积为2,此时D点坐标为(4,6).
解答: 解:(1)∵B点的坐标为B(8,0),
∴﹣16+8b+4=0,解得b=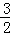 ,
,
∴抛物线的解析式为y═﹣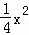 +
+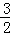 x+4,
x+4,
对称轴方程为x=﹣ =3;
=3;
(2)∵由(1)知,抛物线的对称轴方程为x=3,B(8,0)
∴A(﹣2,0),C(0,4),
∴OA=2,OC=4,OB=8,
∴tan∠ACO=tan∠CBO= ,
,
∴∠ACO=∠CBO.
∵∠AOC=∠COB=90°,
∴△AOC∽△COB.
(3)设BC解析式为y=kx+b,
把(8,0),(0,4)分别代入解析式得,
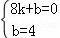 ,解得
,解得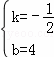 ,
,
解得y=﹣ x+4,
x+4,
作DH⊥x轴,交BC于H.
设D(t,﹣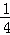 t2+
t2+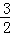 t+4),H(t,﹣
t+4),H(t,﹣ t+4),
t+4),
S△BCD= DH•OB=
DH•OB= ×(﹣
×(﹣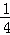 t2+
t2+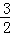 t+4+
t+4+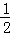 t﹣4)=﹣
t﹣4)=﹣ t2+t=﹣
t2+t=﹣ (t2﹣8t+42﹣16)=﹣
(t2﹣8t+42﹣16)=﹣ (t﹣4)2+2,
(t﹣4)2+2,
当t=4时,△DBC的最大面积为2,此时D点坐标为(4,6).


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
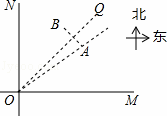
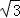 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .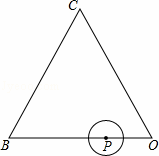
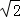 ,求正方形ADCE周长.
,求正方形ADCE周长.
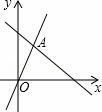
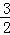 B. x<3 C. x>
B. x<3 C. x>