题目内容
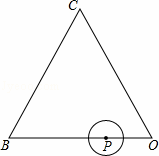
如图,等边三角形OBC的边长为10,点P沿O→B→C→O的方向运动,⊙P的半径为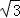 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
6 2
考点: 直线与圆的位置关系;轨迹.
分析: 当点P在OB上且与边OC相切时,作PH⊥OC于H,根据直线与圆相切的判定得到PH=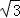 ,再根据等边三角形的性质得∠O=60°,在Rt△OPH中,利用含30度的直角三角形三边的关系得到OH=
,再根据等边三角形的性质得∠O=60°,在Rt△OPH中,利用含30度的直角三角形三边的关系得到OH=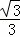 PH=1,OP=2OH=2,即点P在OB,OP=2时,⊙P与边OC相切,然后利用同样的方法可得BP=2或CP=2时,⊙P与△OBC的边相切.
PH=1,OP=2OH=2,即点P在OB,OP=2时,⊙P与边OC相切,然后利用同样的方法可得BP=2或CP=2时,⊙P与△OBC的边相切.
解答: 解:当点P在OB上且与边OC相切时,如图所示:
作PH⊥OC于H,则PH=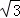 ,
,
∵△OBC为等边三角形,
∴∠O=60°,
在Rt△OPH中,OH=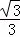 PH=1,
PH=1,
OP=2OH=2,
∴点P在OB,OP=2时,⊙P与边OC相切,
同理可得点P在OB,BP=2时,⊙P与边BC相切;
点P在BC,BP=2时,⊙P与边OB相切,
点P在BC,CP=2时,⊙P与边OC相切,
点P在OC,CP=2时,⊙P与边BC相切,
点P在OC,OP=2时,⊙P与边OB相切,
综上所述,⊙P运动一圈与△OBC的边相切6次,每次相切时,点P分别距离△OBC的顶点2个单位;
故答案为:6;2.

点评: 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.直线l和⊙O相交⇔d<r;直线l和⊙O相切⇔d=r;直线l和⊙O相离⇔d>r.也考查了等边三角形的性质.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目


 B.
B.  C.
C.  D.
D. 
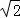 ≈1.414,
≈1.414,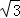 ≈1.732)
≈1.732)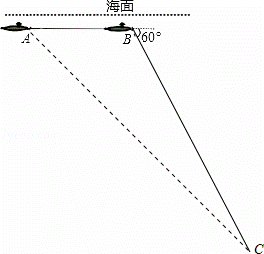
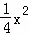 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).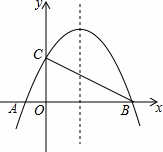
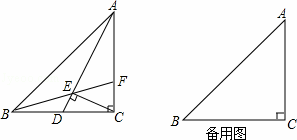
 BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.
BC,连接AD,CE⊥AD于点E,延长线BE交AC于点F.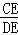 = ,
= ,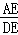 = ;
= ;