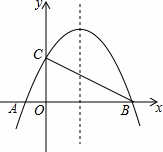题目内容
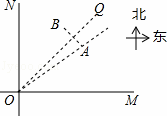
如图,某城市中心的两条公路OM和ON,其中OM为东西走向,ON为南北走向,A、B是两条公路所围区域内的两个标志性建筑.已知A、B关于∠MON的平分线OQ对称.OA=1000米,测得建筑物A在公路交叉口O的北偏东53.5°方向上.
求:建筑物B到公路ON的距离.
(参考数据:sin53.5°=0.8,cos53.5°=0.6,tan53.5°≈1.35)
考点: 解直角三角形的应用-方向角问题.
分析: 连结OB,作BD⊥ON于D,AC⊥OM于C,则∠CAO=∠NOA=53.5°,解Rt△AOC,求出AC=OA•cos53.5°=600米,再根据AAS证明△AOC≌△BOD,得出AC=BD=600米,即建筑物B到公路ON的距离为600米.
解答: 解:如图,连结OB,作BD⊥ON于D,AC⊥OM于C,则∠CAO=∠NOA=53.5°,
在Rt△AOC中,∵∠ACO=90°,
∴AC=OA•cos53.5°=1000×0.6=600(米),
OC=OA•sin53.5°=1000×0.8=800(米).
∵A、B关于∠MON的平分线OQ对称,
∴∠QOM=∠QON=45°,
∴OQ垂直平分AB,
∴OB=OA,
∴∠AOQ=∠BOQ,
∴∠AOC=∠BOD.
在△AOC与△BOD中,
 ,
,
∴△AOC≌△BOD(AAS),
∴AC=BD=600米.
即建筑物B到公路ON的距离为600米.

点评: 本题考查了解直角三角形的应用﹣方向角问题,轴对称的性质,全等三角形的判定与性质,准确作出辅助线证明△AOC≌△BOD是解题的关键.

练习册系列答案
相关题目
 的垂直平分线DE与直线AB相交于点D,垂足为E,连接CD,已知AD=10cm,tan∠ADE=
的垂直平分线DE与直线AB相交于点D,垂足为E,连接CD,已知AD=10cm,tan∠ADE= ,则AC的长度是 .
,则AC的长度是 .
 B.
B.  C.
C.  D.
D. 
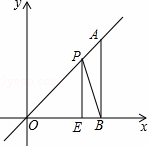
 B. 4+
B. 4+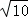 C. 6 D. 4
C. 6 D. 4
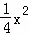 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).