题目内容
已知a-b=5，ab=7，求：
（1）a2+b2；
（2）a+b；
（3）a3+b3．
（1）a2+b2；
（2）a+b；
（3）a3+b3．
考点：立方公式,完全平方式
专题：计算题
分析：（1）由完全平方公式变形得a2+b2=（a-b）2+2ab，结合条件就可求出a2+b2的值．
（2）运用完全平方公式可得（a+b）2=（a-b）2+4ab，结合条件就可求出a+b的值．
（3）运用立方和公式a3+b3=（a+b）（a2-ab+b2）就可求出a3+b3的值．
（2）运用完全平方公式可得（a+b）2=（a-b）2+4ab，结合条件就可求出a+b的值．
（3）运用立方和公式a3+b3=（a+b）（a2-ab+b2）就可求出a3+b3的值．
解答：解：（1）a2+b2=（a-b）2+2ab=25+14=39．
（2）∵（a+b）2=（a-b）2+4ab=25+28=53．
∴a+b=±
．
（3）a3+b3
=（a+b）（a2-ab+b2）
=±
×（39-7）
=±32
．
（2）∵（a+b）2=（a-b）2+4ab=25+28=53．
∴a+b=±
| 53 |
（3）a3+b3
=（a+b）（a2-ab+b2）
=±
| 53 |
=±32
| 53 |
点评：本题主要考查了完全平方公式、立方和公式的灵活运用，需要注意的是一个数的平方等于一个正数，这个数有两个，不要出现遗漏．
练习册系列答案
名校课堂系列答案
相关题目
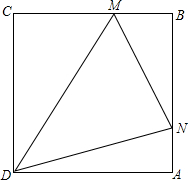已知，边长为a（cm）的正方形ABCD，现有∠MDN=45°，其两边分别与CB、AB交与点M、N，连接MN，将∠MDN绕着顶点D旋转且使得M、N始终在边CB和边AB上，试判断在这一过程中，△BMN的周长是否发生变化，若没有变化，请求出其周长；若发生变化，请说明理由．
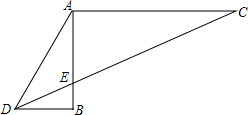已知，如图AC、BD都垂直于AB，且CD交AB于E，CE=2AD，求证：∠ADE=2∠BDE．