题目内容
在平面直角坐标系内有一个△ABC，已知A（0，2）、B（2
，0）、C（m，1）．若S△ABC=4
，求m的值．
| 3 |
| 3 |
考点：坐标与图形性质,三角形的面积
专题：计算题
分析：作CD⊥y轴于D，如图，根据三角形面积公式和利用S△AOB+S△ABC=S梯形BCDO+S△ADC得到关于m的绝对值方程，然后解方程即可
解答：
解：如图，作CD⊥y轴于D，
∵S△AOB+S△ABC=S梯形BCDO+S△ADC，
∴
×2×2
+4
=
（2
+|m|）×1+
×1×|m|，
∴|m|=5
，
∴m=±5
．
解：如图，作CD⊥y轴于D，∵S△AOB+S△ABC=S梯形BCDO+S△ADC，
∴
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∴|m|=5
| 3 |
∴m=±5
| 3 |
点评：本题考查了坐标与图形的性质：利用点的坐标求出相应的线段长和判断线段与坐标轴的位置关系．也考查了三角形的面积．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
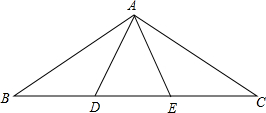组合作交流的时候对下面一道题产生了争议：如图，在△ABC中，点D、B在BC上，∠B=∠C，∠ADE=∠AED=2∠B，由这些条件，你能得出哪些结论？请证明结论． 
如图，△ABC中，AB=AC，BD⊥AC，垂足为D点，AE平分∠BAC，交BD于F，交BC于E，点G为AB上的一点，连接DG，交AE于点H，AG=2，DG=2，AD=2