题目内容
16.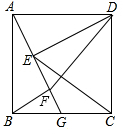 如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.(1)求证:AE=BF;
(2)如图,连接DF、CE,探究线段DF与CE的关系并证明.
分析 (1)根据垂直的定义和平行线的性质求出∠AED=∠BFA=90°,根据正方形的性质可得AB=AD,∠BAD=∠ADC=90°,再利用同角的余角相等求出∠BAF=∠ADE,然后利用“角角边”证明△AFB和△DEA全等,根据全等三角形对应边相等可得AE=BF;
(2)根据同角的余角相等求出∠FAD=∠EDC,根据全等三角形对应边相等可得AF=DE,根据正方形的性质可得AD=CD,然后利用“边角边”证明△FAD和△EDC全等,根据全等三角形对应边相等可得DF=CE,全等三角形对应角相等可得∠ADF=∠DCE,再求出∠DCF+∠CDF=90°,然后根据垂直的定义证明即可.
解答 解:
(1)证明:∵DE⊥AG于点E,BF∥DE且交AG于点F,
∴BF⊥AG于点F,
∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,
∴AB=AD且∠BAD=∠ADC=90°,
∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△AFB和△DEA中,
$\left\{\begin{array}{l}{∠AED=∠BFA=90°}\\{∠BAF=∠ADE}\\{AB=AD}\end{array}\right.$,
∴△AFB≌△DEA(AAS),
∴BF=AE;
(2)DF=CE且DF⊥CE.
理由如下:∵∠FAD+∠ADE=90°,∠EDC+∠ADE=∠ADC=90°,
∴∠FAD=∠EDC,
∵△AFB≌△DEA,
∴AF=DE,
又∵四边形ABCD是正方形,
∴AD=CD,
在△FAD和△EDC中,
$\left\{\begin{array}{l}{AF=DE}\\{∠FAD=∠EDC}\\{AD=CD}\end{array}\right.$,
∴△FAD≌△EDC(SAS),
∴DF=CE且∠ADF=∠DCE,
∵∠ADF+∠CDF=∠ADC=90°,
∴∠DCE+∠CDF=90°,
∴DF⊥CE.
点评 本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,三角形的面积,熟记性质并确定出三角形全等的条件是解题的关键.

| A. | 1+a不是一个代数式 | |
| B. | 0是一个单项式 | |
| C. | 一个多项式的次数为5,那么这个多项式的各项的次数都小于5 | |
| D. | 单项式-$\frac{2πa{b}^{2}}{3}$的系数是-$\frac{2}{3}$ |
| A. | -6 | B. | 9 | C. | -9 | D. | $-\frac{1}{9}$ |
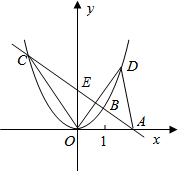 如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).
如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).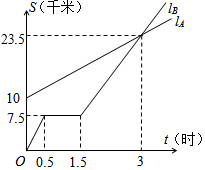 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
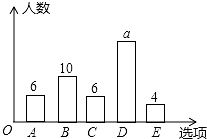 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )
为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )