题目内容
5.计算下列各题:(1)(-$\frac{a}{b}$)2•($\frac{b}{{a}^{2}}$)2+(-2ab)2
(2)(x+3+$\frac{16}{x-5}$)+$\frac{x-1}{5-x}$.
分析 (1)根据分式乘除法法则即可化简运算.
(2)根据因式分解以及分式的基本性质即可化简运算.
解答 解:(1)原式=$\frac{{a}^{2}}{{b}^{2}}•\frac{{b}^{2}}{{a}^{4}}$•$\frac{1}{4{a}^{2}{b}^{2}}$
=$\frac{1}{4{a}^{4}{b}^{2}}$
(2)原式=($\frac{{x}^{2}-2x-15}{x-5}$+$\frac{16}{x-5}$)•$\frac{5-x}{x-1}$
=-$\frac{{(x-1)}^{2}}{x-5}$•$\frac{x-5}{x-1}$
=1-x
点评 本题考查分式的混合运算,解题的关键是熟练运用因式分解以及分式的基本性质,本题属于基础题型.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
15.若14x6y2与-31x3my2的和是单项式,则式子12m-24的值是( )
| A. | -3 | B. | -5 | C. | -4 | D. | 0 |
10.下列给出的数轴中正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列各数是无理数的是( )
| A. | 3.14 | B. | -$\sqrt{9}$ | C. | π | D. | $\frac{22}{7}$ |
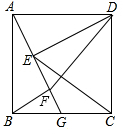 如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.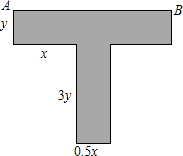 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: 由5个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )
由5个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )