题目内容
6.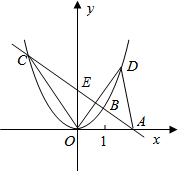 如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).
如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B、C两点,点B的坐标为(1,1).(1)求直线AB和抛物线y=ax2的解析式;
(2)求点C的坐标,求S△BOC;
(2)若抛物线上在第一象限内有一点D,使得S△AOD=S△BOC,求点D的坐标.
分析 (1)根据点A、B的坐标,利用待定系数法即可求出直线AB的解析式,根据点B的坐标利用待定系数法即可求出抛物线的解析式;
(2)连线两函数解析式成方程组,解之即可得出点C的坐标,将x=0代入直线AB的解析式中求出点E的坐标,根据三角形的面积公式即可得出S△BOC的值;
(3)设点D的坐标为(m,m2)(m>0),根据三角形的面积公式结合S△AOD=S△BOC,即可得出关于m的一元二次方程,解之即可得出m的值,取其正值代入点D的坐标中即可得出结论.
解答 解:(1)设直线AB的解析式为y=kx+b(k≠0),
将A(2,0)、B(1,1)代入y=kx+b中,
$\left\{\begin{array}{l}{2k+b=0}\\{k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-x+2.
∵点B(1,1)在抛物线y=ax2上,
∴1=a,
∴抛物线的解析式为y=x2.
(2)联立两函数解析式成方程组,$\left\{\begin{array}{l}{y={x}^{2}}\\{y=-x+2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=4}\end{array}\right.$,
∴点C的坐标为(-2,4).
当x=0时,y=-x+2=2,
∴直线AB与y轴的交点E的坐标为(0,2),
∴OE=2,
∴S△BOC=$\frac{1}{2}$OE•|xC-xB|=$\frac{1}{2}$×2×3=3.
(3)设点D的坐标为(m,m2)(m>0),
∵点A(2,0),
∴OA=2.
∵S△AOD=S△BOC=$\frac{1}{2}$OA•yD=$\frac{1}{2}$×2m2=3,
∴m=$\sqrt{3}$或m=-$\sqrt{3}$(舍去),
∴点D的坐标为($\sqrt{3}$,3).
点评 本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、一次函数图象上点的坐标特征、二次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出函数解析式;(2)联立两函数解析式成方程组,通过解方程组求出点C的坐标;(3)根据面积公式列出关于m的一元二次方程.

| A. | 23 | B. | 29 | C. | 3×23 | D. | 3×6 |
| A. | $\frac{36c}{27{a}^{3}}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a+{b}^{2}}$ | ||
| C. | $\frac{x-1}{1-{x}^{2}}$ | D. | $\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}{-b}^{2}}$ |

| A. | 2n | B. | 2n+1 | C. | 2n-1 | D. | 3n. |
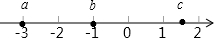 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )| A. | a=-3 | B. | b=-1 | ||
| C. | a的相反数大于b的相反数 | D. | c可能等于2.5 |
| A. | -3 | B. | -5 | C. | -4 | D. | 0 |
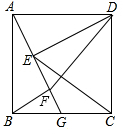 如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.