题目内容
7.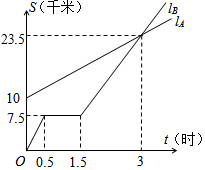 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距10千米.
(2)走了一段路后,自行车发生故障,进行修理,修车所用的时间是1小时.
(3)B从开始出发经过3小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(要求:前3个小题可直接填空,第4小题要写出解答过程)
分析 (1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5-0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)S和t的函数关系是一次函数,设函数是为S=kx+t,过(0,10)和(3,23.5),从而可求出关系式.
解答 解:(1)B出发时与A相距10千米.
(2)修理自行车的时间为:1.5-05=1小时.
(3)B从开始出发经过3小时时与A相遇.
(4)设函数是为S=kx+t,且过(0,10)和(3,23.5),则
$\left\{\begin{array}{l}{t=10}\\{3k+t=23.5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=4.5}\\{t=10}\end{array}\right.$.
故A行走的路程S与时间t的函数关系式为S=4.5x+10.
点评 本题考查一次函数的应用,关键从图象上获取信息,根据图象的确定函数形式,设出函数式,代入已知点确定函数式,求变量或函数值或交点.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
17.下列各式中,不能约分的分式是( )
| A. | $\frac{36c}{27{a}^{3}}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a+{b}^{2}}$ | ||
| C. | $\frac{x-1}{1-{x}^{2}}$ | D. | $\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}{-b}^{2}}$ |
15.若14x6y2与-31x3my2的和是单项式,则式子12m-24的值是( )
| A. | -3 | B. | -5 | C. | -4 | D. | 0 |
17.下列各数是无理数的是( )
| A. | 3.14 | B. | -$\sqrt{9}$ | C. | π | D. | $\frac{22}{7}$ |
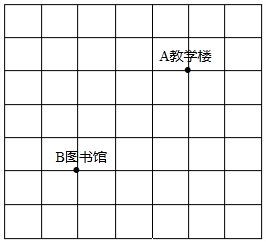 2016年8月31日,东明一中新校区启用,学校迎来高一新生,为了保证新生顺利入学.学校在校园内设立了团员“迎接接待站”,并向家长和学生提供“学校建筑分布图,协助新生完成报到流程,尽全力提供周到的服务,如图为分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(-2,-1),解答以下问题:
2016年8月31日,东明一中新校区启用,学校迎来高一新生,为了保证新生顺利入学.学校在校园内设立了团员“迎接接待站”,并向家长和学生提供“学校建筑分布图,协助新生完成报到流程,尽全力提供周到的服务,如图为分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(-2,-1),解答以下问题: 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.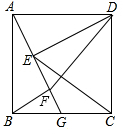 如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
如图,四边形是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.