题目内容
3.若$\frac{y+z-x}{x+y+z}$=$\frac{z+x-y}{y+z-x}$=$\frac{x+y-z}{z+x-y}$=p,则p+p2+p3的值为1.分析 根据$\frac{y+z-x}{x+y+z}$=$\frac{z+x-y}{y+z-x}$=$\frac{x+y-z}{z+x-y}$=p,三式相乘得到$\frac{x+y-z}{x+y+z}$=p3,两式相乘得到$\frac{z+x-y}{x+y+z}$=p2,再把$\frac{y+z-x}{x+y+z}$=p代入p+p2+p3求值即可.
解答 解:∵$\frac{y+z-x}{x+y+z}$=$\frac{z+x-y}{y+z-x}$=$\frac{x+y-z}{z+x-y}$=p,
∴$\frac{(y+z-x)(z+x-y)(x+y-z)}{(x+y+z)(y+z-x)(z+x-y)}$=p3,
$\frac{x+y-z}{x+y+z}$=p3,
$\frac{(y+z-x)(z+x-y)}{(x+y+z)(y+z-x)}$=p2,
$\frac{z+x-y}{x+y+z}$=p2,
∴p+p2+p3
=$\frac{y+z-x}{x+y+z}$+$\frac{z+x-y}{x+y+z}$+$\frac{x+y-z}{x+y+z}$
=$\frac{y+z-x+z+x-y+x+y-z}{x+y+z}$
=$\frac{x+y+z}{x+y+z}$
=1.
故答案为:1.
点评 考查了比例的性质,关键是得到p+p2+p3=$\frac{y+z-x}{x+y+z}$+$\frac{z+x-y}{x+y+z}$+$\frac{x+y-z}{x+y+z}$.

练习册系列答案
相关题目
14.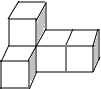 如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )
如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )
 如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )
如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )| A. | 主视图是轴对称图形 | B. | 左视图是轴对称图形 | ||
| C. | 俯视图是轴对称图形 | D. | 三个视图都不是轴对称图形 |
 如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?
如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船? 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0) 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-3,0),B两点,四边形ABCD是边长为4的正方形,且抛物线的顶点E落在过B的直线1上.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-3,0),B两点,四边形ABCD是边长为4的正方形,且抛物线的顶点E落在过B的直线1上.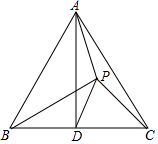 如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.
如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$. 如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米.
如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米. 如图,一条船从灯塔C南偏东42°的A处出发,以每小时8海里的速度向正北航行到达B处,灯塔C在B的北偏西84°方向且距离B处16海里,则船从A到B航行了2小时.
如图,一条船从灯塔C南偏东42°的A处出发,以每小时8海里的速度向正北航行到达B处,灯塔C在B的北偏西84°方向且距离B处16海里,则船从A到B航行了2小时.