题目内容
11. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)(1)直接用含t的代数式分别表示:QB=12-2t,PD=$\frac{4}{3}$t;
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,t的值为3.6秒;若不存在,t的值填“0”.
分析 (1)根据BQ=BC-CQ,表示出QB,由PD与BC平行,根据平行得比例表示出PD的长即可;
(2)存在t,使四边形PDBQ为平行四边形,若四边形PDBQ为平行四边形,得到BQ=PD,求出t的值即可;
解答 解:(1)QB=12-2t,
∵PD∥BC,
∴$\frac{PD}{BC}$=$\frac{AP}{AC}$,
则 $\frac{PD}{12}$=$\frac{t}{9}$,
解得:PD=$\frac{4}{3}$t;
故答案为:12-2t; $\frac{4}{3}$t;
(2)存在,
理由:∵PD∥BC,当PD=BQ时四边形PDBQ为平行四边形,
∴12-2t=$\frac{4}{3}$t,
解得:t=3.6(秒),
∴当t=3.6秒时,四边形PDBQ为平行四边形;
故答案为3.6秒.
点评 本题考查坐标与图形性质,平行四边形的判定与性质,平行线的性质等知识,解本题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.在某次体育测试中,九年级(2)班6位同学的立定跳远成绩(单位:米)分别是:1.83,1.85,1.96,2.08,1.85,1.98,则这组数据的众数是( )
| A. | 1.83 | B. | 1.85 | C. | 2.08 | D. | 1.96 |
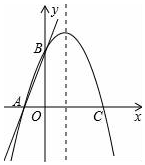 如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).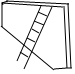 (1)如图,长3m的梯子斜靠着墙,梯子底端离墙底0.6m,问梯子顶端离地面多少米?(精确到0.1m)
(1)如图,长3m的梯子斜靠着墙,梯子底端离墙底0.6m,问梯子顶端离地面多少米?(精确到0.1m)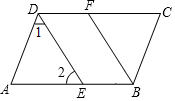 如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.
如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB. 观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;
观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;