题目内容
11. 如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )
如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
分析 过C作CM∥直线l,根据等边三角形性质求出∠ACB=60°,根据平行线的性质求出∠1=∠MCB,∠2=∠ACM,即可求出答案.
解答 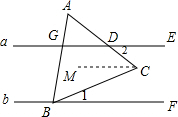 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴∠ACB=60°,
过C作CM∥直线l,
∵直线l∥直线m,
∴直线l∥直线m∥CM,
∵∠ACB=60°,∠1=20°,
∴∠1=∠MCB=20°,
∴∠2=∠ACM=∠ACB-∠MCB=60°-20°=40°,
∴∠ADG=∠2=40°
故选C.
点评 本题考查了平行线的性质,等边三角形的性质的应用,解此题的关键是能正确作出辅助线,注意:两直线平行,内错角相等.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
8.某次捐款活动中,7位同学的捐款金额分别是5元,6元,6元,7元,8元,9元,10元,则这组数据的中位数与众数分别是( )
| A. | 6,6 | B. | 7,6 | C. | 7,8 | D. | 6,8 |
3.假设你班有男生24名,女生26名,班主任要从班里任选一名“社区服务”志愿者,则选中男生的概率是( )
| A. | $\frac{12}{25}$ | B. | $\frac{13}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{50}$ |
20.$\frac{1}{2}$sin60°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\sqrt{3}$ |
 如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°.
如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°.
 如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF为⊙O的切线,交AC于点F.
如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF为⊙O的切线,交AC于点F. 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.