题目内容
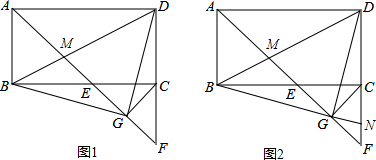
6.平行四边形ABCD中,∠BCD=90°,AE平分∠BAD交BC于点E,交DC的延长线于点F,交BD于M,点G为EF的中点,连接CG、BG、DG.(1)求证:△DCG≌△BEG;
(2)若AB=$\sqrt{2}$CG,DC=2,求MG;
(3)在(2)的条件下,延长BG交DF于N,求△NCG的内切圆半径.
分析 (1)欲证明△DCG≌△BEG,只要证明BE=CD,∠BEG=∠DCG=135°,EG=GC即可.
(2)欲求MG,因为MG=AF-AM-FG,所以想办法求出AM、FG、AF即可解决问题.
(3)作GK⊥CF于K,设△CGN内切圆半径为r,根据$\frac{1}{2}$•CN•GK=$\frac{1}{2}$(CG+CN+GN)•r,只要求出CN、GN、CG、GK即可解决问题.
解答 (1)证明:如图1中,∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠ABC=∠BCD=90°,AD
∵EA平分∠BAD,
∴∠BAE=∠DAE=∠AEB=∠CEF=45°,
∵∠BCF=90°,
∴∠F=∠CEF=45°,
∴AB=BE=CD,CE=CF
∵EG=GF,∠ECF=90°,
∴EG=CG=FG,∠ECG=∠GCF=45°,
∴∠BEG=∠GCD=135°,
在△BEG和△DCG中,
$\left\{\begin{array}{l}{BE=DC}\\{∠BEG=∠DCG}\\{EG=CG}\end{array}\right.$,
∴△DCG≌△BEG.
(2)如图1中,∵AB=$\sqrt{2}$CG,DC=2,
∴AB=CD=2,CG=EG=GF=$\sqrt{2}$,
∴EC=CF=2,
∴AB=CF=DC=2,AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=4$\sqrt{2}$,
∵AB∥DF,
∴$\frac{AM}{MF}$=$\frac{AB}{DF}$,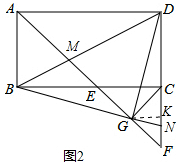
∴AM=$\frac{1}{3}$AF=$\frac{4\sqrt{2}}{3}$,
∴MG=AF=AM-FG=$\frac{5\sqrt{2}}{3}$.
(3)如图2中,作GK⊥CF于K.
∵AB∥NF,
∴$\frac{NF}{AB}$=$\frac{GF}{AG}$=$\frac{GN}{BG}$=$\frac{1}{3}$,
∴NF=$\frac{2}{3}$,CN=CF-NF=$\frac{4}{3}$,
在RT△BCN中,NB=$\sqrt{B{C}^{2}+C{N}^{2}}$=$\frac{4\sqrt{10}}{3}$,
∴GN=$\frac{1}{4}$NB=$\frac{\sqrt{10}}{3}$,
在RT△CGK中,∵∠GCK=45°,CG=$\sqrt{2}$,
∴CK=GK=1,设△CGN内切圆半径为r,
则有:$\frac{1}{2}$•CN•GK=$\frac{1}{2}$(CG+CN+GN)•r,
∴r=$\frac{4}{3\sqrt{2}+\sqrt{10}+4}$.
点评 本题考查圆的综合题、矩形的性质、全等三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,记住三角形内切圆半径的求法,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| 班级 | 七(1) | 七(2) | 七(3) | 七(4) | 七(5) | 七(6) | 七(7) | 七(8) | 七(9) | 七(10) |
| 得分 | 85 | 90 | 90 | 100 | 80 | 100 | 90 | 80 | 85 | 90 |
(2)学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组,小明、小红分别是七(4)班和七(6)班代表队的学生,用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少?
 如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )
如图,直线a∥b,等边三角形ABC的顶点B在直线b上,∠CBF=20°,则∠ADG的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
| A. | 0.25×105 | B. | 2.5×104 | C. | 25×104 | D. | 2.5×105 |
 如图,在平面直角坐标系中,抛物线y=a(x-1)2-4a(a>0)交x轴于A、B两点,点A在点B的左边,其顶点为点C,一条开口向下的抛物线经过A、B、D三点,其顶点D在x轴上方,且其纵坐标为3,连接AC、AD、CD.
如图,在平面直角坐标系中,抛物线y=a(x-1)2-4a(a>0)交x轴于A、B两点,点A在点B的左边,其顶点为点C,一条开口向下的抛物线经过A、B、D三点,其顶点D在x轴上方,且其纵坐标为3,连接AC、AD、CD. 在平面直角坐标系中,直线y=-$\frac{3}{5}x$+3与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
在平面直角坐标系中,直线y=-$\frac{3}{5}x$+3与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.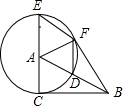 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.