题目内容
5.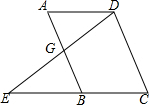 (1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD
(1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD证明:∵AB∥CD已知
∴∠ABE=∠C(两直线平行,同位角相等)
∵∠A=∠C已知
∴∠ABE=∠A(等量代换)
∴BC∥AD(内错角相等,两直线平行)
(2)请写出问题(1)的逆命题并判断他是真命题还是假命题,真命题请写出证明过程,假命题举出反例.
分析 (1)利用平行线的性质,由AB∥CD得到∠ABE=∠C,再利用∠A=∠C得到∠ABE=∠A,然后根据平行线的判定方法可判断BC∥AD;
(2)(1)的逆命题为:已知:如图所示,BC∥AD,∠A=∠C,求证:AB∥CD,它为真命题,同(1)的证明方法一样.
解答 (1)证明:∵AB∥CD(已知)
∴∠ABE=∠C(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠ABE=∠A(等量代换)
∴BC∥AD(内错角相等,两直线平行)
故答案为∠C,两直线平行,同位角相等;
(2)(1)的逆命题为:
已知:如图所示,BC∥AD,∠A=∠C,求证:AB∥CD.(它为真命题)
证明:∵BC∥AD(已知)
∴∠ABE=∠A(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠ABE=∠C(等量代换)
∴AB∥CD(内错角相等,两直线平行).
点评 本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.也考查了平行线的判定与性质.

练习册系列答案
相关题目
15.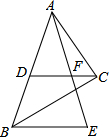 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
13.下列说法正确的是( )
| A. | 无限小数是无理数 | B. | $\sqrt{16}$的平方根是±4 | ||
| C. | -6是(-6)2的一个算术平方根 | D. | -5的立方根是$\root{3}{-5}$ |
20.小明的身高不低于1.7米,设身高为h米,用不等式可表示为( )
| A. | h>1.7 | B. | h<17 | C. | h≤1.7 | D. | h≥1.7 |
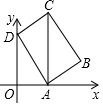 如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.
如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴.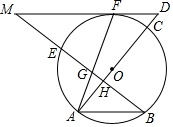 如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.
如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG. 如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$.
如图,从数轴的原点O向右数出3个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为$\sqrt{10}$. 直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.
直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.