题目内容
14.观察下列各个等式的规律:第一个等式:$\frac{{{2^2}-{1^2}-1}}{2}$=1,第二个等式:$\frac{{{3^2}-{2^2}-1}}{2}$=2,第三个等式:$\frac{{{4^2}-{3^2}-1}}{2}$=3…
请用上述等式反映出的规律解决下列问题:
(1)直接写出第四个等式;
(2)猜想第n个等式(用n的代数式表示),并证明你猜想的等式是正确的.
分析 (1)根据题目中的式子的变化规律可以写出第四个等式;
(2)根据题目中的式子的变化规律可以猜想出第n个等式并加以证明.
解答 解:(1)由题目中式子的变化规律可得,
第四个等式是:$\frac{{5}^{2}-{4}^{2}-1}{2}=4$;
(2)第n个等式是:$\frac{(n+1)^{2}-{n}^{2}-1}{2}=n$,
证明:∵$\frac{(n+1)^{2}-{n}^{2}-1}{2}$
=$\frac{[(n+1)+n][(n+1)-n]-1}{2}$
=$\frac{2n+1-1}{2}$
=$\frac{2n}{2}$
=n,
∴第n个等式是:$\frac{(n+1)^{2}-{n}^{2}-1}{2}=n$.
点评 本题考查规律型:数字的变化类,解答本题的关键是明确题目中式子的变化规律,求出相应的式子.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列从左到右的变形是因式分解的是( )
| A. | ab-b=b(a-1) | B. | (m+n)(m-n)=m2-n2 | C. | -10x-10=-10(x-1) | D. | x2-2x+1=x(x-2)+1 |
12.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形①平行四边形;②菱形;③对角线互相垂直的四边形;④对角线相等的四边形,满足条件的是( )
| A. | ①③④ | B. | ②③ | C. | ①②④ | D. | ①②③ |
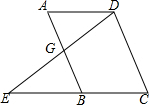 (1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD
(1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD