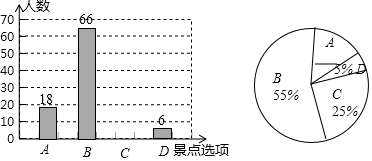
题目内容
15.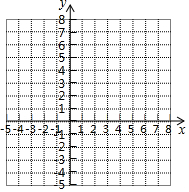 直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.
直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.(1)写出A,B两点的坐标,并画出直线l的图象;
(2)将直线l向上平移4个单位得到l1,l1交x轴于点C.作出l1的图象,l1的解析式是y=-2x+6.
(3)将直线l绕点A顺时针旋转90°得到l2,l2交l1于点D.作出l2的图象,tan∠CAD=$\frac{1}{2}$.
分析 (1)分别令x=0求得y、令y=0求得x,即可得出A、B的坐标,从而得出直线l的解析式;
(2)将直线向上平移4个单位可得直线l1,根据“上加下减”的原则求解即可得出其解析式;
(3)由旋转得出其函数图象及点B的对应点坐标,待定系数法求得直线l2的解析式,继而求得其与y轴的交点,根据tan∠CAD=tan∠EAO=$\frac{OE}{OA}$可得答案.
解答 解:(1)当y=0时,-2x+2=0,解得:x=1,即点A(1,0),
当x=0时,y=2,即点B(0,2),
如图,直线AB即为所求;
(2)如图,直线l1即为所求,
直线l1的解析式为y=-2x+2+4=-2x+6,
故答案为:y=-2x+6;
(3)如图,直线l2即为所求,
方法一、∵直线l绕点A顺时针旋转90°得到l2,
∴∠BAD=90°,
∴∠CAD+∠OAB=90°,
又∵∠OAB+∠ABO=90°,
∴∠CAD=∠ABO,
∴tan∠CAD=tan∠ABO=$\frac{OA}{OB}$=$\frac{1}{2}$;
方法二:∵直线l绕点A顺时针旋转90°得到l2,
∴由图可知,点B(0,2)的对应点坐标为(3,1),
设直线l2解析式为y=kx+b,
将点A(1,0)、(3,1)代入,得:$\left\{\begin{array}{l}{k+b=0}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴直线l2的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,
当x=0时,y=-$\frac{1}{2}$,
∴直线l2与y轴的交点E(0,-$\frac{1}{2}$),
∴tan∠CAD=tan∠EAO=$\frac{OE}{OA}$=$\frac{\frac{1}{2}}{1}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查一次函数图象与几何变换及一次函数图象,熟练掌握平移变换和旋转变换的性质及待定系数法求函数解析式是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | ①③④ | B. | ②③ | C. | ①②④ | D. | ①②③ |
| 解:原式=2x2-1-x(x+5)…① =2x2-1-x2+5x…② =x2+5x-1 …③ |
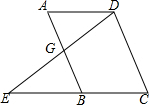 (1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD
(1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD