题目内容
15.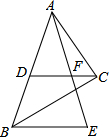 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
分析 先根据直角三角形的性质求出CD的长,再由三角形中位线定理即可得出结论.
解答 解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,
∴CD=$\frac{1}{2}$AB=4.5.
∵CF=$\frac{1}{3}$CD,
∴DF=$\frac{2}{3}$CD=$\frac{2}{3}$×4.5=3.
∵BE∥DC,
∴DF是△ABE的中位线,
∴BE=2DF=6.
故选A.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
相关题目
 在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是26分.
在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是26分.
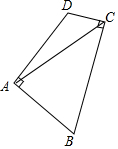 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.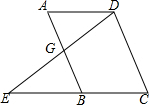 (1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD
(1)已知:如图所示,AB∥CD,∠A=∠C,求证:BC∥AD