题目内容
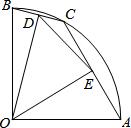 如图,在扇形OAB中,∠AOB=90°,点C是
如图,在扇形OAB中,∠AOB=90°,点C是 |
| AB |
 |
| AB |
考点:垂径定理,等腰直角三角形,三角形中位线定理
专题:
分析:连接AB,先根据垂径定理得出D、E分别是线段BC与AC的中点,故可得出DE是△ABC的中位线,故可得出AB的长,再根据勾股定理求出OA的长即可.
解答: 解:连接AB,
解:连接AB,
∵OD⊥BC,OE⊥AC,
∴D、E分别是线段BC与AC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=4.
∵Rt△OAB中,OA=OB,
∴OA=
=
=2
.
故答案为:2
.
 解:连接AB,
解:连接AB,∵OD⊥BC,OE⊥AC,
∴D、E分别是线段BC与AC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=4.
∵Rt△OAB中,OA=OB,
∴OA=
|
|
| 2 |
故答案为:2
| 2 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列黑色粗体英文字母是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
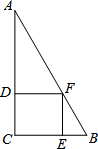 如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D、E、F分别在边AC、BC、AB上,如果AC=10,BC=6,那么正方形DCEF的边长为
如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D、E、F分别在边AC、BC、AB上,如果AC=10,BC=6,那么正方形DCEF的边长为
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是