题目内容
已知直线l与直线y=2x+1的交点横坐标是2,与直线y=-x+2的交点纵坐标为1,求直线l与两坐标轴围成的三角形的面积.
考点:两条直线相交或平行问题
专题:
分析:首先根据“直线l与直线y=2x+1的交点横坐标是2,与直线y=-x+2的交点纵坐标为1”确定直线经过的点的坐标,从而利用待定系数法确定一次函数的解析式,然后求得与坐标轴的交点坐标,从而求得与坐标轴的围成的三角形的面积.
解答:解:∵直线l与直线y=2x+1的交点横坐标是2,与直线y=-x+2的交点纵坐标为1,
∴直线l与直线y=2x+1的交点纵坐标y=2×2+1=5,与直线y=-x+2的交点横坐标为1,
∴直线l经过点(2,5)和(1,1),
设直线l的解析式为y=kx+b,
∴
解得:
∴直线l的解析式为y=4x-3,
令y=4x-3=0,
解得:x=
,
令x=0,解得:x=-3,
∴直线l与两坐标轴的交点坐标为(
,0),与y轴的交点为(0,-3),
∴直线l与两坐标轴围成的三角形的面积
×
×3=
.
∴直线l与直线y=2x+1的交点纵坐标y=2×2+1=5,与直线y=-x+2的交点横坐标为1,
∴直线l经过点(2,5)和(1,1),
设直线l的解析式为y=kx+b,
∴
|
解得:
|
∴直线l的解析式为y=4x-3,
令y=4x-3=0,
解得:x=
| 3 |
| 4 |
令x=0,解得:x=-3,
∴直线l与两坐标轴的交点坐标为(
| 3 |
| 4 |
∴直线l与两坐标轴围成的三角形的面积
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
点评:本题考查了两条直线相交或平行问题,解题的关键是能够利用待定系数法确定一次函数的解析式,难道不大.

练习册系列答案
相关题目
已知xm=6,xn=3,则xm+2n的值为( )
| A、9 | B、6 | C、54 | D、81 |
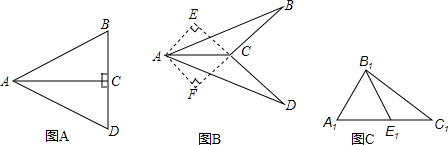
 如图,在扇形OAB中,∠AOB=90°,点C是
如图,在扇形OAB中,∠AOB=90°,点C是
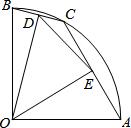
 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2
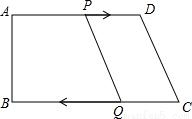 已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=26,点P从A点出发,沿AD边以1个单位的速度向点D运动,点Q从点C开始沿CB边以3个单位的速度向点B运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.
已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=26,点P从A点出发,沿AD边以1个单位的速度向点D运动,点Q从点C开始沿CB边以3个单位的速度向点B运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.