题目内容
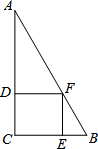如图，已知在Rt△ABC中，∠C=90°，正方形DCEF的顶点D、E、F分别在边AC、BC、AB上，如果AC=10，BC=6，那么正方形DCEF的边长为考点：相似三角形的判定与性质,正方形的性质
专题：
分析：证明△ADF∽△ACB，列出比例式即可解决问题．
解答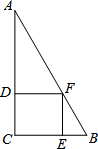：解：∵四边形DCEF为正方形，
∴DF∥BC，DC=DF（设为λ），
∴△ADF∽△ACB，AD=10-λ，
∴AD：AC=DF：BC，而BC=6，
即（10-λ）：10=λ：6，
解得：λ=
，
故答案为
．
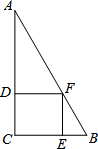解：∵四边形DCEF为正方形，∴DF∥BC，DC=DF（设为λ），
∴△ADF∽△ACB，AD=10-λ，
∴AD：AC=DF：BC，而BC=6，
即（10-λ）：10=λ：6，
解得：λ=
| 15 |
| 4 |
故答案为
| 15 |
| 4 |
点评：该题主要考查了相似三角形的判定及其性质、正方形的性质等几何知识点的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合运用能力提出了一定的要求．
练习册系列答案
相关题目
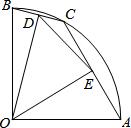如图，在扇形OAB中，∠AOB=90°，点C是
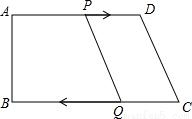已知直角梯形ABCD中，AD∥BC，∠B=90°，AB=8，AD=24，BC=26，点P从A点出发，沿AD边以1个单位的速度向点D运动，点Q从点C开始沿CB边以3个单位的速度向点B运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t．