题目内容
9. 如图,在△ABC中,D为BC上一点,∠BAD=∠ABC,∠ADC=∠ACD,若∠BAC=60°.试求∠DAC,∠ADC的度数.
如图,在△ABC中,D为BC上一点,∠BAD=∠ABC,∠ADC=∠ACD,若∠BAC=60°.试求∠DAC,∠ADC的度数.
分析 设∠BAD=x,则∠CAD=60°-x,∠ABC=∠BAD=x,由∠ADC=∠ACD,故∠ADC=∠ACD=$\frac{180°-∠CAD}{2}$=$\frac{180°-(60°-x)}{2}$=$\frac{120°+x}{2}$,再由三角形内角和定理即可得出结论.
解答 解:∵∠BAC=60°,∠BAD=∠ABC,
∴设∠BAD=x,则∠CAD=60°-x,∠ABC=∠BAD=x,
∵∠ADC=∠ACD,
∴∠ADC=∠ACD=$\frac{180°-∠CAD}{2}$=$\frac{180°-(60°-x)}{2}$=$\frac{120°+x}{2}$,
在△ABC中,
∵∠ACD+∠ABC+∠BAC=180°,即$\frac{120°+x}{2}$+x+60°=180°,解得x=40°,
∴∠DAC=60°-40°=20°,∠ADC=$\frac{120°+x}{2}$=$\frac{120°+40°}{2}$=80°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
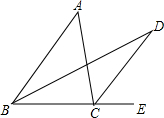 如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?
如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?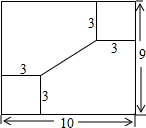 如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.
如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm. 如图,一个四边形木框,四边长分别为AB=8,BC=6,CD=4,AD=5,它的形状是不稳定的,求AC和BD的取值范围.
如图,一个四边形木框,四边长分别为AB=8,BC=6,CD=4,AD=5,它的形状是不稳定的,求AC和BD的取值范围.