题目内容
 如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为
如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为考点:正方形的性质
专题:
分析:设正方形ABCD的边长为a,正方形AEFG的边长为b,表示出BE,再根据正方形的性质表示出CF,然后相比计算即可得解.
解答:解:设正方形ABCD的边长为a,正方形AEFG的边长为b,
则BE=a-b,
∵正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,
∴点F在正方形ABCD的对角线上,
∴CF=
a-
b,
∴BE:CF=(a-b):(
a-
b)=
.
故答案为:
.
则BE=a-b,
∵正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,
∴点F在正方形ABCD的对角线上,
∴CF=
| 2 |
| 2 |
∴BE:CF=(a-b):(
| 2 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了正方形的性质,主要利用了正方形的对角线与边长的关系,难点在于判断出点F在正方形ABCD的对角线上.

练习册系列答案
相关题目
下列运动形式属于旋转的是( )
| A、钟表上钟摆的摆动 |
| B、投篮过程中球的运动 |
| C、“神十”火箭升空的运动 |
| D、传动带上物体位置的变化 |
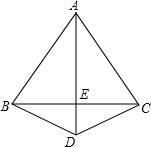 如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE=
如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE= 如图,正比例函数y=2x的图象与反比例函数y=
如图,正比例函数y=2x的图象与反比例函数y=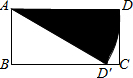 如图,在矩形ABCD中,AB=1,AD=2,将AD边绕点A顺时针旋转,使点D恰好落在BC边上的D′处,则阴影部分的扇形面积为( )
如图,在矩形ABCD中,AB=1,AD=2,将AD边绕点A顺时针旋转,使点D恰好落在BC边上的D′处,则阴影部分的扇形面积为( ) 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=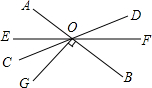 如图,已知直线AB、CD、EF相交于点O,GO⊥AB,∠DOB是它余角的2倍.∠AOE=2∠DOF.
如图,已知直线AB、CD、EF相交于点O,GO⊥AB,∠DOB是它余角的2倍.∠AOE=2∠DOF.