题目内容
 如图,正比例函数y=2x的图象与反比例函数y=
如图,正比例函数y=2x的图象与反比例函数y=| k |
| x |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:
分析:先把x=
代入y=2x求出y的值得到A点的坐标,再把A点的坐标代入y=
求出k的值,得到反比例函数的解析式,进而将两函数解析式联立得出B点坐标即可.
| 3 |
| k |
| x |
解答:解:∵正比例函数y=2x的图象与反比例函数y=
的图象相交于A,B两点,其中,点A的横坐标为
,
∴当x=
时y=2
,
∴A(
,2
).
把A(
,2
)代入y=
得,
k=
×2
=6,
所以反比例函数解析式为y=
.
解方程组
,得
,
,
∴点B的坐标为:(-
,-2
).
故答案为:(-
,-2
).
| k |
| x |
| 3 |
∴当x=
| 3 |
| 3 |
∴A(
| 3 |
| 3 |
把A(
| 3 |
| 3 |
| k |
| x |
k=
| 3 |
| 3 |
所以反比例函数解析式为y=
| 6 |
| x |
解方程组
|
|
|
∴点B的坐标为:(-
| 3 |
| 3 |
故答案为:(-
| 3 |
| 3 |
点评:此题主要考查了一次函数与反比例函数的交点问题,根据已知得出A点坐标是解题关键.本题求出A点的坐标以后,还可以根据正比例函数与反比例函数的交点关于原点对称直接得到B点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点C是AB的中点,点D是BC的中点,AB=28,求线段AD的长.
如图,点C是AB的中点,点D是BC的中点,AB=28,求线段AD的长. 如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,求证:BH=AC.
如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,求证:BH=AC. 如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是
如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是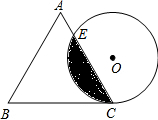 如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E. 如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为
如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为 如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形.
如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形. 如图:E、F是线段AC、AB的中点,且BC=6cm.求线段EF的长.
如图:E、F是线段AC、AB的中点,且BC=6cm.求线段EF的长.