题目内容
 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=| k |
| x |
(1)求边AB的长;
(2)求反比例函数的解析式和点F的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先根据E点坐标求出OA的长,再由AO=2AB即可得出边AB的长;
(2)先得出B点坐标,再由中点坐标公式求出D点坐标,将D点坐标代入y=
,利用待定系数法求出反比例函数解析式,再由点F在BC上,得出点F的纵坐标为2,把y=2代入反比例函数解析式,得出x的值,即可确定点F的坐标.
(2)先得出B点坐标,再由中点坐标公式求出D点坐标,将D点坐标代入y=
| k |
| x |
解答:解:(1)∵E(4,n),
∴OA=4,
∵AO=2AB,
∴AB=2;
(2)∵OA=4,AB=2,
∴B(4,2),
∵点D为OB的中点,
∴D(2,1),
∵点D在反比例函数y=
的图象上,
∴1=
,即k=2,
∴反比例函数的关系式为y=
,
∵点F在BC上,
∴点F的纵坐标为2,
把y=2代入y=
,得x=1,
∴点F的坐标为(1,2).
∴OA=4,
∵AO=2AB,
∴AB=2;
(2)∵OA=4,AB=2,
∴B(4,2),
∵点D为OB的中点,
∴D(2,1),
∵点D在反比例函数y=
| k |
| x |
∴1=
| k |
| 2 |
∴反比例函数的关系式为y=
| 2 |
| x |
∵点F在BC上,
∴点F的纵坐标为2,
把y=2代入y=
| 2 |
| x |
∴点F的坐标为(1,2).
点评:此题考查了反比例函数与一次函数的交点问题,坐标与图形性质,中点坐标公式,待定系数法确定反比例解析式,函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,在函数y1=
如图,在函数y1=| k1 |
| x |
| k2 |
| x |
| 1 |
| 2 |
| 9 |
| 2 |
A、
| ||||
| B、5 | ||||
C、
| ||||
D、
|
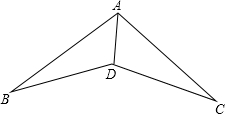 如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )| A、∠B=∠C,BD=DC |
| B、∠ADB=∠ADC,BD=DC |
| C、∠B=∠C,∠BAD=∠CAD |
| D、BD=DC,AB=AC |

 如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是
如图,△ABC与△CDE都是正三角形,图中可以通过旋转而相互得到到的三角形是 如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为
如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为 如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形.
如图,点D是△ABC中BC边上的中点,连接AD并延长使DE=AD,连接BE.请指出图中成中心对称的线段、三角形,并写出面积相等的三角形.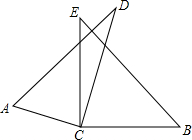 如图,将两块直角三角尺的直角顶点C叠放在一起
如图,将两块直角三角尺的直角顶点C叠放在一起 如图:E、F是线段AC、AB的中点,且BC=6cm.求线段EF的长.
如图:E、F是线段AC、AB的中点,且BC=6cm.求线段EF的长.