题目内容
18.计算(1)($\sqrt{2}+\sqrt{3}$)×$\sqrt{3}$
(2)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
(3)(π+1)0-$\sqrt{12}$+|-$\sqrt{3}$|
(4)(4+3$\sqrt{5}$)2.
分析 (1)直接根据二次根式乘法运算法则得出答案;
(2)首先化简二次根式,进而得出答案;
(3)首先化简二次根式以及结合零指数幂的性质和绝对值的性质化简,进而得出答案;
(4)直接利用完全平方公式化简求出答案.
解答 解:(1)($\sqrt{2}+\sqrt{3}$)×$\sqrt{3}$
=$\sqrt{6}$+3;
(2)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(3)(π+1)0-$\sqrt{12}$+|-$\sqrt{3}$|
=1-2$\sqrt{3}$+$\sqrt{3}$
=1-$\sqrt{3}$;
(4)(4+3$\sqrt{5}$)2
=16+45+24$\sqrt{5}$
=61+24$\sqrt{5}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | AB∥CD,∠A=∠C | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠D=∠B |
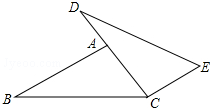 如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.
如图,点D、A、C在同一直线上,AB∥CE,AB=CD,∠B=∠D,求证:BC=DE.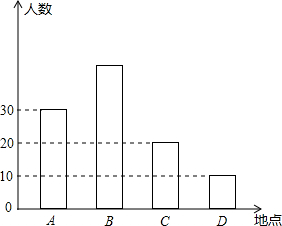 暑假快要到了,某市准备组织同学们分别到A、B、C、D四个地方进行夏令营活动,前往四个地方的人数如图所示:
暑假快要到了,某市准备组织同学们分别到A、B、C、D四个地方进行夏令营活动,前往四个地方的人数如图所示: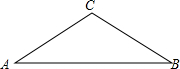 如图,已知在等腰△ABC中,∠A=∠B=30°.
如图,已知在等腰△ABC中,∠A=∠B=30°.