题目内容
3.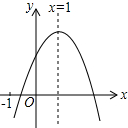 如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )
如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 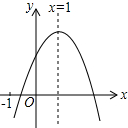 解:①抛物线开口方向向下,则a<0.
解:①抛物线开口方向向下,则a<0.
抛物线对称轴在y轴的右侧,则a、b异号,所以ab<0.
又∵抛物线与y轴交于正半轴,则c>0,
∴abc<0,故①错误;
②如图所示,当x=0时,y>0,则根据抛物线的对称性知,当x=2时,y>0,即4a+2b+c>0.
故②正确;
③如图所示,∵当x=-1时,y<0,对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a,则-3a-c=-(a-b+c)>0,即-3a-c>0,
即3a+c<0,故③正确;
④⑤∵x=1时,y=a+b+c(最大值),
x=m时,y=am2+bm+c,
∵m≠1的实数,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b)成立.
∴④正确.
综上所述,正确的结论有3个.
故选:C.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.精确到十分位( )
| A. | 13.42 | B. | 134.20 | C. | 1.342 | D. | 1342.0 |
 二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.
二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.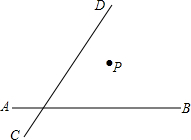 如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线.
如图所示,P为马厩,AB为草地边缘(下方为草地),CD为一河流,牧人欲从马厩牵马先去草地吃草,然后到河边饮水,最后回到马厩,请帮他确定一条最佳行走路线. 如图,⊙O的半径为5cm,AB、AC是⊙O的两条弦,AB=6$\sqrt{2}$cm,AC=8cm.过点O作一个圆与AC相切,则这个圆的半径是多少?它与AB具有怎样的位置关系?为什么?
如图,⊙O的半径为5cm,AB、AC是⊙O的两条弦,AB=6$\sqrt{2}$cm,AC=8cm.过点O作一个圆与AC相切,则这个圆的半径是多少?它与AB具有怎样的位置关系?为什么?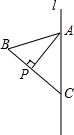 如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.
如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.