题目内容
18. 二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.
二次函数y=x2+bx的图象如图,对称轴为x=-2.若关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则t的取值范围是-4≤t<12.
分析 先利用对称轴方程求出b得到抛物线解析式为y=x2+4x,再配成顶点式得到抛物线的顶点坐标为(-2,-4),接着根据二次函数的性质,运用函数图象求出当-5<x<2时,对应的函数值的范围为-4≤y<12,由于关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解,则抛物线y=x2+bx与直线y=t有交点,然后借助图象可得到-4≤t<12.
解答 解:∵-$\frac{b}{2×1}$=-2,解得b=4,
∴抛物线解析式为y=x2+4x,即y=(x+2)2-4,
∴抛物线的顶点坐标为(-2,-4),
当x=2时,y=x2+4x=12,
∴当-5<x<2,-4≤y<12,
∵一元二次方程x2+bx-t=0(t为实数)的解可看作抛物线y=x2+bx与直线y=b的交点的横坐标,
∴关于x的一元二次方程x2+bx-t=0(t为实数)在-5<x<2的范围内有解时,抛物线y=x2+bx与直线y=t有交点,如图,
∴-4≤t<12.
故答案为-4≤t<12.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可转化为解关于x的一元二次方程.也考查了二次函数的性质和二次函数与一次函数图象的交点问题.运用数形结合的思想是解决本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
9.如图图案是我国几家银行的标志,其中轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.计算(-0.25)2014×(-4)2015+(-1)2015+12015的结果为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 1 |
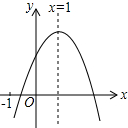 如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )
如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )