题目内容
12.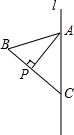 如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.
如图,已知△ABC点AC在直线l上,∠B=60°,∠ACB=50°,AP⊥BC,垂足为P.(1)试在图中作出△ABC关于直线l对称的图形△ADC;
(2)求∠BCD的度数并确定P点的对称点E点,直接写出∠PAE的度数.
分析 (1)过点B作AC的垂线,垂足为H,延长BH到D,使DH=BH,则可得到△ADC与△ABC关于l对称;
(2)根据对称的性质得∠ACD=∠ACB=50°,则∠BCD=2∠ACB=100°;在CD上截取CE=CP,则可判断点E为P点的对称点,所以∠EAC=∠PAC,然后利用互余计算出∠PAC,从而可得到∠PAE的度数.
解答 解:(1)如图,△ADC为所作;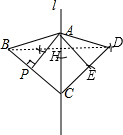
(2)∵△ADC与△ABC关于l对称,
∴∠ACD=∠ACB=50°,
∴∠BCD=2∠ACB=100°,
在CD上截取CE=CP,则点E为P点的对称点;
∴∠EAC=∠PAC,
∵AP⊥BC,
∴∠APC=90°,
∴∠PAC=90°-∠ACP=40°,
∴∠PAE=2∠PAC=80°.
点评 本题考查了作图-轴对称变换:几何图形都可看做是有点组成,在画一个图形的轴对称图形时,先从确定一些特殊的对称点开始的,一般的方法是:由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
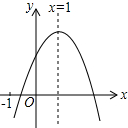 如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )
如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( ) 如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,且AD=1,CD=3,求直径AB的长.
如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,且AD=1,CD=3,求直径AB的长.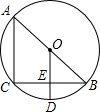 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.