题目内容
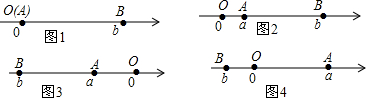
14.阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是4,数轴上表示1和-3的两点之间的距离是4;
(2)数轴上表示x和3的两点A和B之间的距离是|x-3|,如果|AB|=2,那么x为1或5;
(3)式子|x+1|+|x-3|的最小值是4.
分析 (1)根据数轴上两点间的距离=两个数之差的绝对值,算出即可;
(2)表示出AB的距离,根据绝对值等于2的数有2或-2两个,解答出即可;
(3)|x+1|+|x-3|的最小值,意思是x到-1的距离与到3的距离之和最小,那么x应在-1和2之间的线段上.
解答 解:(1)数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
(2)数轴上表示x和3的两点A和B之间的距离是|x-3|,如果|AB|=2,那么x为1或5;
(3)当-1≤x≤3时,|x+1|+|x-3|的最小值是4.
故答案为:(1)3,3,4;(2)|x-3|,1或5,(3)4.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值,绝对值是正数的数有2个.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
9.如图图案是我国几家银行的标志,其中轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.在平面直角坐标系中,设A(-1,-2),B(4,-1),C(m,0),D(n,n)为四边形的四个顶点,当四边形ABCD的周长最短时,$\frac{m}{n}$的值为( )
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 1 |
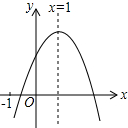 如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )
如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )