题目内容
已知抛物线y=ax2+bx+c经过点A(1,0),B(0,-5),C(2,3).
(1)求抛物线的解析式及其顶点坐标;
(2)若点E(m,y1)、F(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
(1)求抛物线的解析式及其顶点坐标;
(2)若点E(m,y1)、F(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:计算题
分析:(1)将A,B,C三点代入解析式求出a,b,c的值,即可确定出解析式,得出顶点坐标;
(2)利用二次函数的单调性判断即可得到结果.
(2)利用二次函数的单调性判断即可得到结果.
解答:解:(1)将点A(1,0),B(0,-5),C(2,3)代入y=ax2+bx+c得:
,
解得:a=-1,b=6,c=-5.
∴抛物线解析式为y=-x2+6x-5,顶点坐标为(3,4);
(2)抛物线解析式为y=-x2+6x-5=-(x-3)2+4,
∵点E(m,y1)、F(n,y2)(m<n<3)都在该抛物线上,且x<3抛物线为增函数,
∴y1<y2.
|
解得:a=-1,b=6,c=-5.
∴抛物线解析式为y=-x2+6x-5,顶点坐标为(3,4);
(2)抛物线解析式为y=-x2+6x-5=-(x-3)2+4,
∵点E(m,y1)、F(n,y2)(m<n<3)都在该抛物线上,且x<3抛物线为增函数,
∴y1<y2.
点评:此题考查了待定系数法求二次函数解析式,以及二次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
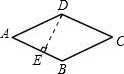 如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积.
如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积. 如图,AD为△ABC的中线,BE⊥AD于E,CF⊥AD于F,求证:DE=DF.
如图,AD为△ABC的中线,BE⊥AD于E,CF⊥AD于F,求证:DE=DF.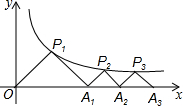 如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=