题目内容
8.如图1,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,求证:GE=BE+GD;
(3)如图2,在直角梯形ABCG中,AG∥BC(BC>AG),∠B=90°,AB=BC=6,E是AB边上一点,且∠GCE=45°,BE=2,求GE的长.
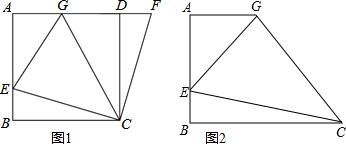
分析 (1)根据正方形的性质得出CB=CD,∠CBE=∠CDF=90°,然后根据SAS证得△CBE≌△CDF,即可证得结论;
(2)首先证得∠GCF=∠GCE=45°,然后根据SAS证得△ECG≌△FCG,即可证得GE=GF=DF+GD=BE+GD;
(3)图2中将梯形ABCG补成图1所示的正方形ABCD,再延长AD到F使得DF=BE,由(1)(2)结论知GE=GD+BE,设GD=x,则AG=6-x,AE=6-2=4,GE=x+2,然后根据勾股定理列出关于x的方程,解方程求得GD的长,即可求得EG的长.
解答  (1)证明:如图1,∵四边形ABCD是正方形,
(1)证明:如图1,∵四边形ABCD是正方形,
∴CB=CD,∠CBE=∠CDF=90°,
在△CBE和△CDF中
$\left\{\begin{array}{l}{CB=CD}\\{∠CBE=∠CDF}\\{DF=BE}\end{array}\right.$
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)证明:∵∠GCE=45°,
∴∠BCE+∠GCD=45°,
由(1)可知△CBE≌△CDF,
∴∠DCF=∠BCE,BE=DF,
∴∠GCF=∠GCD+∠DCF=45°,
在△ECG和△FCG中
$\left\{\begin{array}{l}{EC=FC}\\{∠GCE=∠GCF=45°}\\{GC=GC}\end{array}\right.$
∴△ECG≌△FCG(SAS),
∴GE=GF=DF+GD=BE+GD,
即GE=BE+GD;
(3)解:图2中将梯形ABCG补成图1所示的正方形ABCD,再延长AD到F使得DF=BE,
由(1)(2)结论知GE=GD+BE,
设GD=x,∵AB=BC=6,BE=2,
∴AG=6-x,AE=6-2=4,GE=x+2,
∵EG2=AG2+AE2,
∴(x+2)2=(6-x)2+42,
解得x=3,
∴GE=BE+GD=2+3=5.
点评 本题考查了正方形的性质,三角形全等的判定和性质以及勾股定理的应用,(3)根据(1)(2)结论将梯形ABCG补成图1所示的正方形是解题的关键.

| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
 如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
如图所示,直线L1的解析式是y=2x-1,直线L2的解析式是y=x+1,则方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$. x^y
x^y